Blog
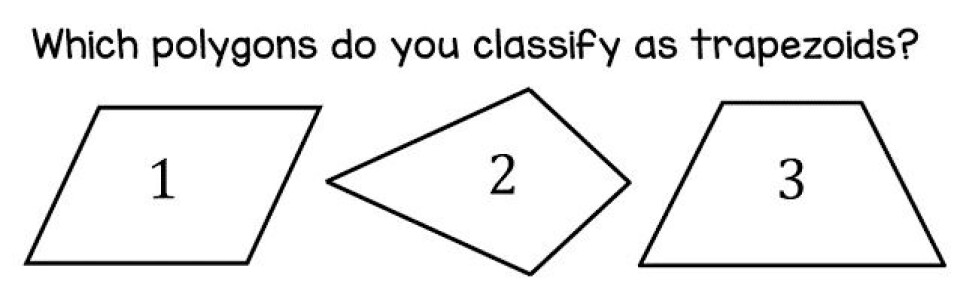
Det er vist en ommer! - Trapezer i folkeskolens formelsamling
I forbindelse med et lektionsstudie er det gået op for mig at trapezer nogle steder defineres anderledes end jeg selv har lært det - og undervist det!
En væsentlig del af et lektionsstudie er det såkaldte "kyozai kenkyuu" - der hvor man studerer eksisterende viden på området.
Sammen med min gode kollega Mia Jürgensen, var vi netop gået startet på det; i forbindelse med at undersøge, hvordan vi bedre kunne komme til at eksemplificere Van Hieles niveauer i vores undervisning.
Jeg nævner, at jeg altid har haft en forkærlighed for at bruge trapezer i mine eksempler, og hertil spørger Mia, om jeg er klar over at disse kan defineres på flere måder!
Det var jeg så godt nok ikke... jeg var helt sikker på at trapezer er firkanter med (mindst) to parallelle sider. (Den såkaldt inkluderende definition)
Det viser sig imidlertid at nogle kan finde på at definere trapezer som firkanter med netop to parallelle sider... deriblandt formelsamlingen for folkeskolen s. 37 (https://www.uvm.dk/-/media/filer/uvm/udd/voksne/pdf17/okt/171026-matematiske-formler-og-fagord.pdf?la=da) (den såkaldt ekskluderende definition)
Selvfølgelig kan man definere ting som man har lyst til i matematik, men efter min mening er det bare ikke særlig hensigtsmæssigt at bruge den ekskluderende definition, specielt hvor man tænker på elevernes videre progression i matematikken. Jeg har udelukkende set den inkluderende definition brugt i ungdomsuddannelse og videregående uddannelse.
Den inkluderede definition har også den fordel, at ting man ved om trapezer så også gælder for parallelogrammer, rektangler og kvadrater. Det ligger i tråd med hvorledes man i øvrigt klassificerer geometriske figurer som delmængder af andre figurklasser.
En ekskluderende definition vil også betyde at anden matematik som fx det bestemte integral vil være udefineret for visse værdier. Den ekskluderende definition fremstår altså som et historisk kuriosum, ikke som noget der passer sammen med resten af matematikken i det 21. århundrede.
Kigger vi på lærerplaner, altså curriculum, lidt ligesom ”Fælles Mål”, anbefales det også i ”Common Core Standards” (Amerikansk National Curriculum) at bruge den inkluderende definition.
Så at have den ekskluderende definition i dansk folkeskole, og tilhørende formelsamling: Det er en ommer!