Addition af brøker

Nedenstående didaktiske idé blev udviklet og afprøvet af et lærerteam og mig i et lektionsstudie med fokus på, hvordan elever kan undersøge sig frem til regnereglen for at lægge brøker sammen. Beskrivelsen er en sammenfatning af afprøvning i 3 klasser. Som det vil fremgå, lykkedes ikke alle elementer af ideen i praksis, og læseren opfordres til at komme med forslag til udvikling af ideen.

Normalt, når vi underviser i addition af brøker, fortæller vi regnereglen, der siger, at når to brøker har samme nævner, lægger man brøkerne sammen ved at lægge deres tællere sammen. Typisk vil vi også forklare det ved et eksempel, fx at hvis Tobias har spist 3 kvarte stykker pizza og Marie har spist 2 kvarte stykker pizza, har de to tilsammen spist 5 kvarte stykker pizza. Til trods for så tydelige eksempler oplever mange af os, at eleverne ikke helt udvikler den forståelse for brøker, som vi have tænkt.

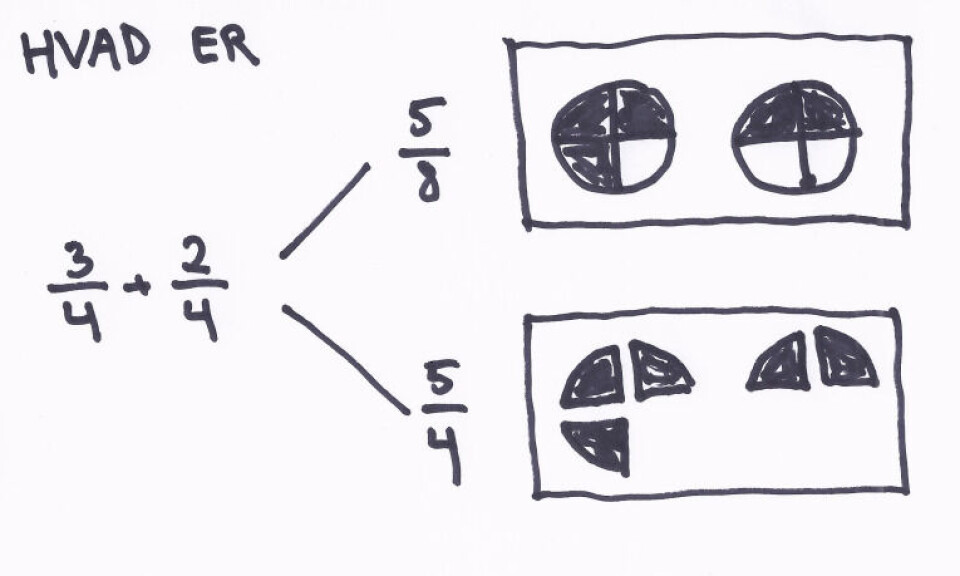
— Læreren starter med at skrive 3/4 på tavlen og spørger, hvad det betyder. Selv om nogle elever nævner både tæller, brøkstreg og nævner, er det centrale her, at få fokus på, hvad 3/4 betyder, altså tre fjerdedele. Når man beder en elev illustrere det på tavlen, vil de typisk gøre det med en pizza delt i fjerdedele, hvor tre af dem er skraverede.

Læreren skriver nu på tavlen: Hvad er 3/4 + 2/4. Stort set alle elever svarer 5/8. Elevernes forudgående viden om hhv. brøker og addition taget i betragtning, er det et helt fornuftigt bud. Og når man spørger eleverne, hvordan de kom frem til det, kan de komme med et rigtig godt argument: Hvis man tegner to cirkler (pizzaer), der hver er delt i fjerdedele og skraverer tre fjeredele i den ene og to fjerdedele i den anden, er der tydeligvis fem ud af otte fjerdedele, der er skraverede.

Hvis der ikke er elever, der mener, at svaret må være 5/4, fortæller læreren den lille hvide løgn, at eleverne i en af de andre klasser var sikre på på, at svaret var 5/4 og spørger, om de kan forestille sig, hvad de mon har tænkt? Hvordan skulle de kunne komme frem til at, at svaret måtte være 5/4?

Ideen med at etablere denne 'konflikt' er, at eleverne bliver nødt til at komme med og lytte til faglige argumenter. Det skal være det stærkeste faglige argument, der 'vinder', og ikke bare lærerens eller en stærk elevs autoritet. En af udfordringerne her var, at ikke mange elever koblede arbejdet med brøker i matematikundervisningen til det, som brøker kan repræsentere i virkeligheden. Fx var der ikke én elev, der tænke på 'virkelige' kvarte stykker pizza. Hvis eleverne tænker på at spise først tre og så to kvarte stykker pizza, er de jo ikke i tvivl om, at de har spist fem kvarte stykker pizza i alt.

Vi ved ikke, hvorfor eleverne ikke koblede til virkeligheden, men vi ved, at det er et generelt problem. Bl.a. kom en skoleleder, fra en af de skoler i landet, hvor elever får de højeste karakterer, med det eksempel, at mange elever i deres 5. og 6. klasse ikke er bevidste om, at en liter mælk i hjemkundskab og en liter mælk i matematik har den samme volumen.

Det ser også ud til, at en af udfordringerne for vores lektion var, at eleverne troede, at i en brøk kan tælleren ikke være større end nævneren. Det 'løste' vi i den sidste (tredje) afprøvning med at starte med regnestykket 1/4 + 2/4. Det gav den ønskede faglige konflikt, men vi havnede i det samme problem med den manglende kobling til virkeligheden - der jo skal bære det afgørende argument.

I stedet for at give eleverne svaret i den pågældende lektion, diskuterede læreren med resten af teamet, om det kunne have været en fordel at tilbyde eleverne en stak kvarte 'pizzastykkker' (fx i pap) og/eller lede eleverne til at opfatte fx 3/4 som 3 seperate fjerdedele.

En anden udfordring vi mødte undervejs var, at nogle elever viste, hvordan de var kommet til 5/8, ved at dele en cirkel op i ottendedele og skravere de fem af dem. Det viser selvfølgelig, hvordan de kan repræsentere deres svar, men det var overraskende, at de brugte det som svar på, hvordan de havde løst den forudgående opgave. Det 'værste' var måske, at ingen af de andre elever gjorde indvendinger mod den frie veksling mellem fjerdedele og ottendedele.

Jeg glæder mig tli at høre, hvordan lærerne efterfølgende fulgte op på den lektion.

Hvis nogle af jer læsere har gode overvejelser om ovenstående, er I meget velkomne til at dele dem med os andre. Vi har to vigtige regler ifm. refleksion af lektioner: Gå efter bolden og bliv på banen. Med andre ord: Hold fokus på elevernes handlingssmuligheder i lektionen og lad være med at komme med helt andre ideer - diskuter den her præsenterede.