Naturen og teknologien

Teknologi bør ikke kun handle om maskiner

Først og fremmest er dette en teknologi-blog. Jeg vil dog komme ind på matematik, men det er på ingen måde mit ærinde at bevise formlerne. Jeg vil også nævne Fibonacci-sekvensen og komme med eksempler på kodning. Men dette skal langt fra ses som nogen guide. 

Derimod håber jeg at mit skriv måske kan være et indspark til, at vi bruger naturen og bevægelsen noget mere. Teknologi skal ingenlunde være fikseret omkring maskiner og computere, som den i høj grad er i dag. Og lad os gerne tænke tværfaglighed ind i teknologien.

I nedenstående tekst nedfælder jeg som sagt et par ord om Fibonacci-sekvensen. Her kunne discipliner som biologi og matematik sagtens komme i spil.

Fibonacci-sekvensen

Jeg vil her komme ganske kort ind på Fibonacci-sekvensen, og hvordan vi kan implementere denne som kode i programmerinssproget Python, hvor vi med relativt få linjers kode kan udregne en række af tallene fra sekvensen.

Hvorfor jeg anbefaler Python skyldes at det er gratis, er et godt, stabilt programmeringssprog som er enkelt at installere, og så er det mit indtryk at stadig flere elever og lærere er blevet bekendte med det. Desuden kan man vha. Mircobits egen editor konvertere sine koder til formatet(hex) som micro:bit kan læse og altså dermed printe Fibonacci-sekvensen på skærmen. Alternativt kan man også bare bruge den editor, IDLE, som kan downloades direkte fra Pythons egen side. 

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 og alle kaninerne

Kort og godt går sekvensen i sin enkelhed ud på, at vi starter sekvensen med 0 og 1. Herefter adderer vi de to tal, der summeret bliver til det næste tal i sekvensen. Lad mig eksemplificere dette:

0 + 1 = 1 

1 + 1 = 2 

2 + 1 = 3

3 + 2 = 5

5 + 3 = 8

8 + 5 = 13

13 + 8 = 21 …

Vi får altså en række af Fibonaccis-sekvensen der ser således ud: 0, 1, 1, 2, 3, 5, 8, 13, 21 … Den fortsætter derudad, så når jeg nævner Fibonacci-sekvensen herinde, mener jeg altså kun dele af den.

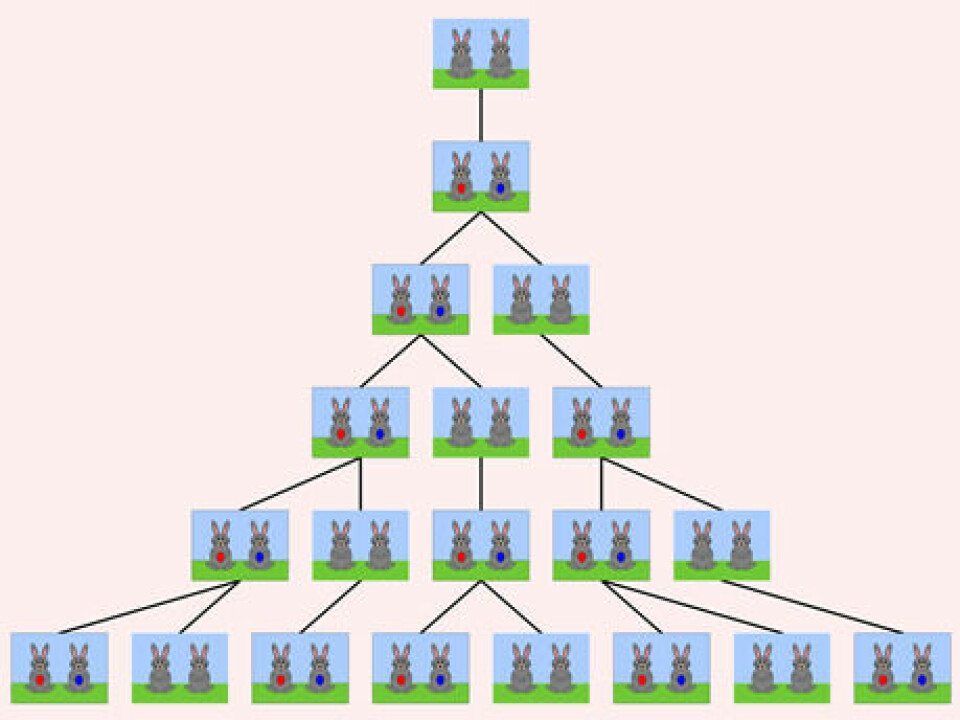
Logikken bag Leonardo Fibonaccis talrække, som blev tænkt for 800 år siden, tager sit udgangspunkt i at et ung-par kaniner først er blevet produktionsdygtige efter en måned, hvorefter storken kommer flyvende med et nyt par unge kaniner den efterfølgende måned. Det nye ung-par reproducerer sig herefter i den efterfølgende måned. Og det samme gør det ældre par kaniner fra tidligere også. Således fortsætter produktionen kontinuerligt deruda. Altså først har vi et par 1 par(ikke kønsmodne) i den første måned, det samme par(nu kønsmodne) i næste måned, måneden efter er der nu 2 par(parret har reproduceret sig), og måneden efter 3 par, den næste måned er der 5 par, og den næste er der 8 par, 13 par osv. Håber ikke den forklaring blev alt for forvirrende.

Kod et Fibonacci-program

Et program som udregner Fibonacci-sekvensen, i Python, kunne se sådan ud:

# Antallet af iterationer af

n = 20

# De foerste to tal i rækken a=0 og b=1

a = 0

b = 1

# Listen til Fibonacci-sekvensen

fib_liste = []

# For loop itererer n antal gange

for i in range(n):

    fib_liste.append(a)

    print("a", a, "b:", b) # Denne linje viser a og b's iteration i loopet. 

    a,b = b,a+b

print()

print(f'De første {n} numre i Fibonacci-sekvensen er, {fib_liste}')

Herefter fortæller Python os:

De første 20 numre i Fibonacci-sekvensen er, [0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181]

Det spændende ved Fibonacci-sekvensen er, at vi ser tallene gå igen i naturen.

Fx har en af iris-arterne(vertosa) 3 kronblade, som ses på nedenstående billede:

Iris Vertosa med de 3 blade.

En Leverurt (Parnassia palustris) har 5 blade

Mens en stolt kavaler har 8 blade.

Dette er ikke bare nogle nøje udvalgte billeder af blomster, som jeg ville klippe hæl og tå af for, at få til at matche fibonacci-sekvensens tal. Prøv selv at gå ud og tæl blade og se om de matcher. 

Man kan altså sagtens gå på opdagelse og finde forskellige bevoksninger som, træer, planter og blomster at finde sekvensen i.

Phyllotaxi

Nu går vi en lille smule ind på phyllotaxiens område. Her kan vi se på hvorledes spiralerne i blomsten er bygget op. I nedenstående eksempel findes der 21 spiraler, som går i den ene retning, mens 13 spiraler går i den modsatte. Altså har vi igen at gøre med tal fra fibonacci-sekvensen. Man kan også beregne vinklen af blomster og blade, som generelt skubber sig med 137,5 graders vinkel fra hinanden.

Det gyldne snit / Phi

Afslutningsvis er det i øvrigt også interessant at iagttage, hvorledes man vha. division af tal i Fibonacci-sekvensen næsten altid kan se forholdet til det gyldne snit/phi, hvor det ene af de to irrationale tal har formlen (1 + sqrt(5)) : 2. Denne angiver tallet 1,618.

Denne formel kunne skrives sådan i python:

# Det gyldne snit

# import af modulet math, da vi skal bruge funktionen sqrt.

import math

# Variabel som udregner phi

phi = (1 + math.sqrt(5)) / 2

# Printer variablen

print(phi)

Dividerer vi tallene fra fibonacci-sekvensen med hinanden får vi nogenlunde det samme forhold til phi: 3:2 = 1,5, 5:3 = 1,666, 8:3 = 1,6. Og så fremdeles. Det beskrives mere udførligt på Math is fun.

Opsummeret

Danske børn er europamestre i skærmbrug. En gennemsnitlige teenager bruger 6 timer foran skærmen(*1). Formandsskabet for rådet for børns læring peger ikke på nogen entydig konsensus om, hvorvidt den megen brug af skærme har positiv eller negativ effekt.

Ifølge Sundhedsstyrelsen(*2) bevæger børn og unge sig for lidt.

Ud fra et sundhedsmæssigt perspektiv giver det i min verden god mening at inddrage naturen mere i undervisningen. En tur i naturen hvor vi laver research og går på opdagelser i botanikkens univers skaber masser af bevægelse.

Det ene behøver jo ikke at udelukke det andet. Jeg synes der er en tendens til at vi kun ser på teknologi, som noget der sker foran en eller anden maskine. Men man kan, som jeg har fremført her, også bruge teknologien, som et redskab til at fremme bevægelse samtidig med at vi nyder en god, sanserig oplevelse i naturen.

Jeg har brugt Fibonacci til at indsamle data i min lille research, men vi kunne også have set på nedbør og vejr eller vandforhold. I øvrigt er Fibonacci langt fra den eneste sekvens, som er at finde i naturen. Der er masser af virkerlig spændende ting at researche på i naturen.

Gode ressourcer:

Dr. Dr. P. Prusinkiewicz  og Astrid Lindenmeyer har bl.a. skrevet en række fine publikationer om, hvordan vi kan modellere naturen vha. algoritmer. Her i blandt publikationen The Algorithmic Beauty of Plants. Publikationerne er gratis og frit til gængelige. Der er masser af virkelig spændende publikationer, som man kan dykke ned i og gå på opdagelse i.

God fornøjelse!

Kilde:

1) https://www.uvm.dk/aktuelt/nyheder/rbl/2020/200320-vi-har-drevet-den-digitale-udvikling-frem-i-bedste-mening--men-det-er-tid-til-at-stoppe-op

2) https://skoleidraet.dk/nyheder/sundhedsstyrelsen-11-15-aarige-bevaeger-sig-for-lidt/