Så upræcise er nationale test

Jeg har fået den ære at få min egen blog på Folkeskolen.dk. Egentlig var det min tanke at skrive om danskfaget og undervisning i litteratur, kommunikation, om grammatik, it, læsning på nettet og den slags. Men nationale test fylder lidt for meget for mig for tiden. Så jeg starter med et indlæg om dem.

Ministeriet har netop udgivet et notat om ”nationale tests reliabilitet”. Det er virkelig oprørende læsning. Men yderst teknisk. Så jeg tænkte jeg ville forsøge at illustrere hvad problemet er.

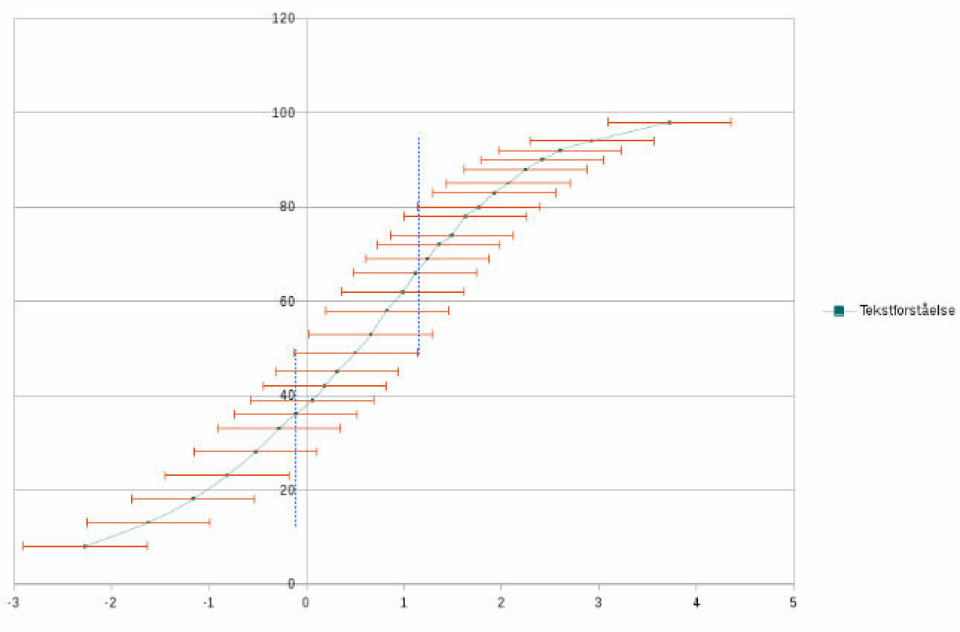
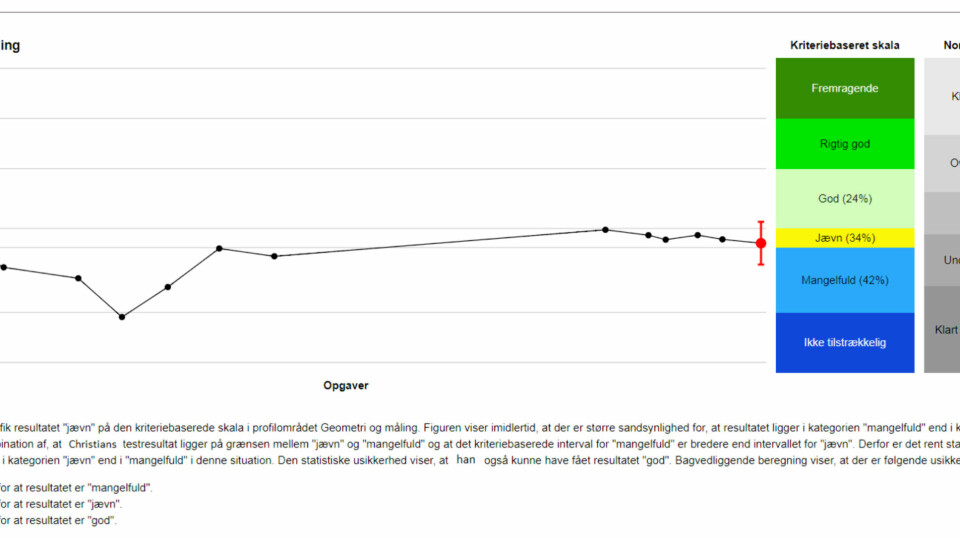
Jeg har i forbindelse med et forskningsprojekt fået adgang til data fra 2. klasse læsning i 2014. Ud fra disse data har jeg konstrueret en ”gennemsnitsklasse” med 27 elever. Jeg har simpelthen valgt hver 2000 elev af de 55000 elever der blev testet i 2. klasse i 2014. Dem har jeg sat ind i et diagram hvor deres præstation på den bagvedliggende skala, logitskalaen, er på x-aksen, og den tilsvarende percentilværdi (den der opgives til elevernes lærer) er på y-aksen.

Alle test har en usikkerhed på beregningen af hver enkelt elevs præstation. Det kaldes Standard Error of Measurement. Den var oprindelig på 0,55, men ministeriet har fortalt mig at de har fået den længere ned. Jeg sætter den til 0,45. Ifølge hjemmesiden rasch.org (http://www.rasch.org/rmt/rmt91c.htm) kan man sammenligne to præstationer med en 2-halet t-test. Det har jeg gjort ved at indsætte vandrette streger af længden 2*0,63 i mit diagram. Hvis to elevers streger ikke overlapper hinanden, kan man sige med 95% sandsynlighed at de har forskellige resultater.

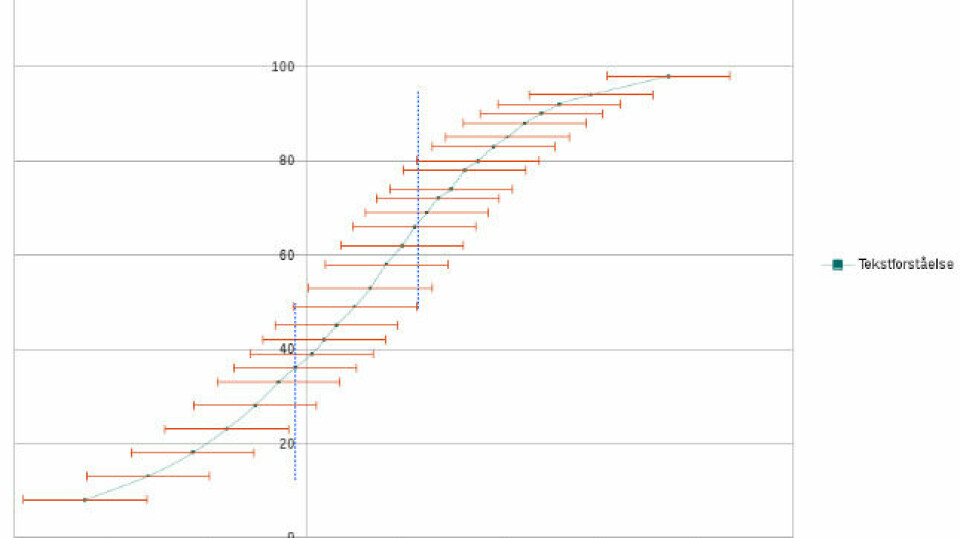
Se diagrammet for tekstforståelse i 2. klasse ovenfor.

Jeg har sat to blå lodrette streger ind for at vise hvilke elever, den elev der har fået omkring 50 på percentilskalaen, statistisk set har samme resultat som. Lad os kalde ham Peter. Som det fremgår, er Peter på samme niveau som 6 elever der har scoret mindre end ham, og 9 elever der har scoret mere. Peter er altså sådan cirka lige så god som 15 af sine klassekammerater. Man kan ikke sige andet end at Peter er bedre end de omkring 25% dårligste procent af eleverne i Danmark, og dårligere ned de omkring 20% af eleverne i Danmark.

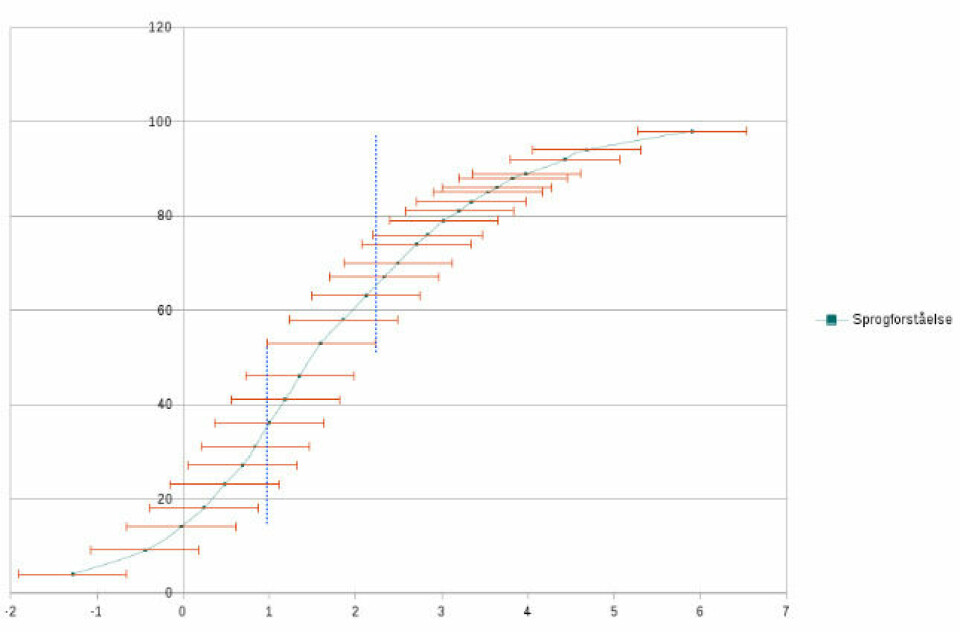
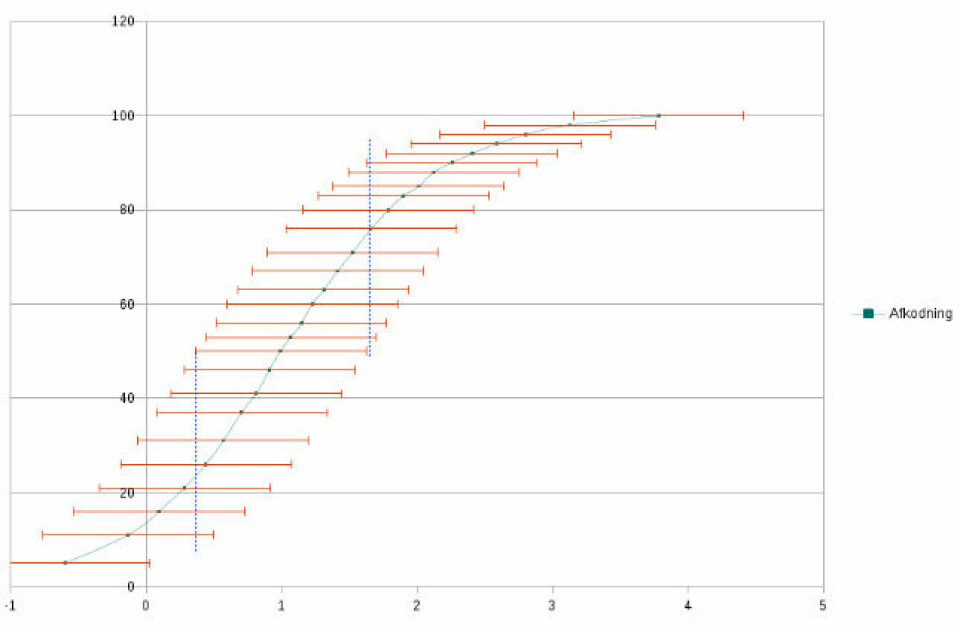
Se også på diagrammerne for sprogforståelse og afkodning.

Som det fremgår, er Peter i sprogforståelse på samme niveau som 6 der er dårligere end ham og 6 der er bedre.

I afkodning er Peter på niveau med 20 af sine klassekammerater. Der er én der er dårligere og 5 der er bedre.

Man kan også sige at den næstedårligste elev, der har opnået 12 point på percentilskalaen i tekstforståelse, måske alligevel ligger på omkring 30-35 point. Eller at den fjerdebedste, der har fået omkring 90 point, måske alligevel kun skulle have haft 70.

Man kan med andre ord ikke bruge nationale test til at sige ret meget om den enkelte elevs niveau.

Så det synes jeg man skulle lade være med.