Line Maj Møller
Blog
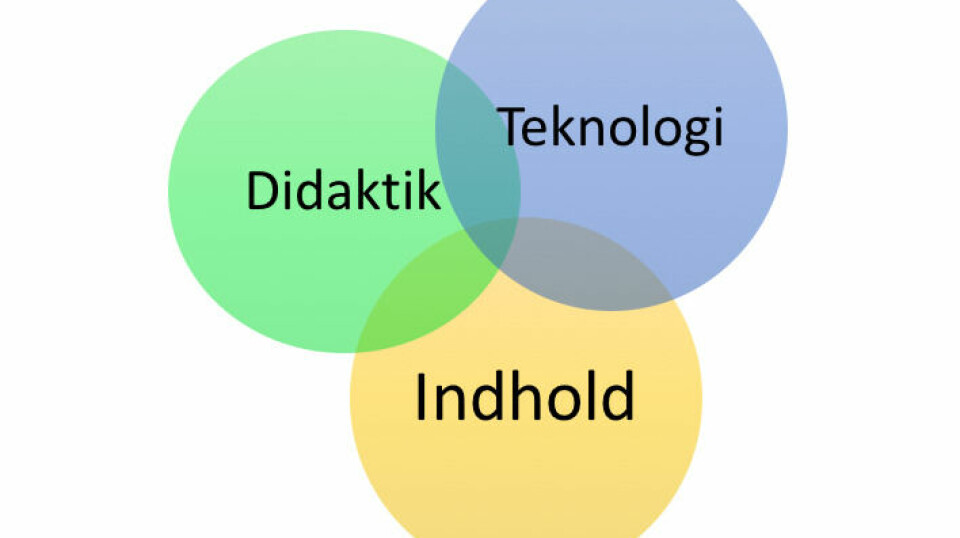
Hvad nu hvis der ikke er nogen løsning?
Menigmand vil højst sandsynlig mene, at det som kendetegner løsning af matematikopgaver er søgen efter ét rigtigt svar. Dette kan der uden tvivl ligge mange årsager til grund for. De som er relativt velbevandret indenfor matematikken kan end dog gå med til at der til en matematikopgave kan findes flere løsninger. Men kan det give mening at arbejde med opgaver i matematik, som ikke har nogen løsning? Og i så fald, hvor ofte gør vi det?
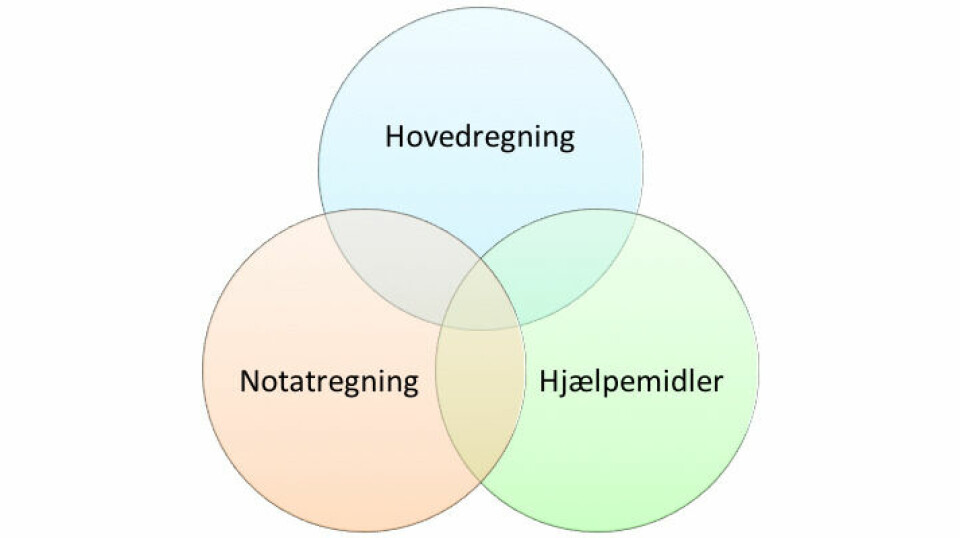
Inden min nyligt overståede barsel havde jeg haft fornøjelsen af min daværende 5.klasse siden de startede i 4.klasse. De udviklede sig aldeles pragtfuldt, hvis I spørger mig, og deres engagement og matematikiver var blandt højdepunkterne på mit ugentlige skema. Klassen var på daværende tidspunkt begyndt at arbejde med månedsopgaver, som afspejlede opgaver med fokus på notatregning (skriftlige regnestrategier), hovedregning, tekstopgaver og sidst men ikke mindst matematiske grublere.
Noget af det jeg havde meget fokus på var netop elevernes evne til og interesse for problemløsning, forstået som evnen til at håndtere og overkomme kognitive frustrationer.
Sædvanligvis var der et kvarters spørgetid om ugen til månedsopgaven, og i uge 2 var køen særlig lang - netop grundet månedens grubler. Gennemgående for spørgsmålene relateret til grubleren var, at eleverne egentlig havde fundet en løsning, men alle var de ved nærmere eftertanke kommet i tvivl. Sideløbende med disse spørgsmål kan man måske levende forestille sig de af klassens ”hurtige heste” som sad indenfor høre-rækkevidde kommentere med: ”Årh ja, den opgave har jeg løst, da var da nem…”
Frøken G stod forrest i køen, og bad mig skrive en talrække ned på et stykke papir, mens hun forklarede at hun troede hun havde fundet en løsning. Efter at have fået hjælp af sin ældre kusine var hun dog alligevel blevet i tvivl. Hun kunne ydermere berette, at kusinen havde sendt et billede af opgaven til sine veninder, som læste til matematiklærere og de kunne heller ikke finde ud af at løse opgaven.
Jeg talte med hende om det interessante i dette, og at hun måske ikke skulle have så meget fokus på løsningen, men hellere fokusere på at få skrevet hendes argumenter ned for, hvorfor hun blev i tvivl om løsningen.
Lille frøken Hansen stod også i spørgsmålskøen, og da det blev hendes tur trak hun mig til side, mens hun med øjne så store som tekopper hviskede til mig: ”… Jeg har fået at vide at opgaven slet ikke har nogen løsning…!!!”
Da jeg svarede, at det da bestemt også var et tænkeligt scenarie er det muligt, at jeg så 50% af frøken Hansens livsgnist sive ud af ørene på hende (sammen med den sidste rest af tiltro til hendes matematiklærer).
Det jeg vil fremhæve med disse små citater er egentlig vigtigheden i at holde fokus på arbejdsproces fremfor resultat, men også det faktum, at vi ikke må reducere matematikfaget til en søgen efter ”den eneste løsning.”
Det er også derfor jeg ikke fremhæver selve opgaven, men derimod processen omkring arbejdet med opgaven. Jeg er både benovet og tilfreds med mine elevers måde at gå til opgaven på, og deres spirende evne til at forholde sig kritisk til det umiddelbare svar. Da rygtet om både muligheden og ræsonnementerne for ”ingen løsning” spredte sig i klassen falmede det kække udtryk i øjnene på nogle af klassens hurtige heste.
(I et andet indlæg kunne det være interessant at præsentere jer for forældrene reaktioner, som krævede et lille frustrationsdæmpende AULA-skriv...)
Jeg er bevidst om, at opgaver uden løsning med jævne mellemrum dukker sporadisk op i vores læremidler, men hvor ofte taler vi eksplicit og helt generelt om muligheden for én, flere eller ingen løsninger? Jeg vil i hvert fald gerne gøre det oftere.
Må kaffen være varm, og jeres WIFI-forbindelse stærk
Line