Line Maj Møller
Blog
Nogle gange skal man vende tingene på hovedet…
... for bedre at kunne forstå! Jeg bliver så trist, når jeg oplever dygtige elever på mellemtrinnet og i udskolingen, som forklarer et lighedstegn som ”det tegn, der står til venstre for facit.” Når lighedstegnet reduceres til at være en indikator for, ”hvor jeg finder facit”, så kan det eksempelvis være svært at forstå ligevægtsprincippet, når det gælder ligningsløsning. Men jeg vil også vove den påstand, at det indsnævrer elevernes talforståelse. I stedet for blot at ”jage et facit” er der utrolig meget undring og læring i at tage sit afsæt i et konkret facit, og undersøge hvilke opgaver man kan opstille til det pågældende facit.
Jeg har i øjeblikket matematik på 9.årgang, hvor emnet er ”ligninger”.Vi arbejder på niveaudelte hold, og jeg sidder for tiden med den stærkeste tredjedel af 9.årgang.
Vi har i de indledende timer arbejdet en del med bevidstgørelse af de forskellige strategier som eleverne bruger. Vi har overordnet skelnet mellem ”gæt”, ”regn baglæns” og ”ligevægtsprincippet”.
Eleverne har arbejdet med forskellige typer af ligninger med et varierende antal led, og hvor der kan indgå parenteser, rødder, brøker o. lign. De har løst ligningerne på fornuftigste vis, og været dygtige til at samtale omkring hvilken strategi, der bruges ”hvornår” og ”hvordan”.
Meget traditionelt har fokus været på at løse ligninger. Forleden vendte vi så emnet på hovedet, og i stedet for at løse ligninger, fik eleverne til opgave at opstille ligninger med en konkret løsning.
Med inspiration fra Pernille Pind skulle eleverne angive tre typer af svar. Det almindelige svar (i dette tilfælde den almindelige ”standard” ligning, som den oftest ser ud i fx færdighedsregninger), det smarte svar (i dette tilfælde den smarte ligning, som er så enkel at man tilnærmelsesvis kan ”se” svaret uden at regne) og endelig – det vanskelige svar (i dette tilfælde den vanskelige ligning, som kan bestå af mange led og hvor man kan udfordre sig selv med både rødder, parenteser, brøker og andre ubehageligheder).
Særligt det vanskelige svar udfordrer elevernes fantasi og kreativitet uanset niveau. Eleverne tvinges til at udfordre og nuancere deres ligningsbegreb, når de skal øge kompleksiteten i en given ligning.
Som lærer var det spændende at observere de forskellige strategier som eleverne benyttede; nogen skrev et tilfældigt udtryk ned og tilpassede så efterhånden på begge sider af lighedstegnet indtil det gik op. Andre elever gik systematisk til værks og startede med løsningen og byggede så op på begge sider af lighedstegnet.
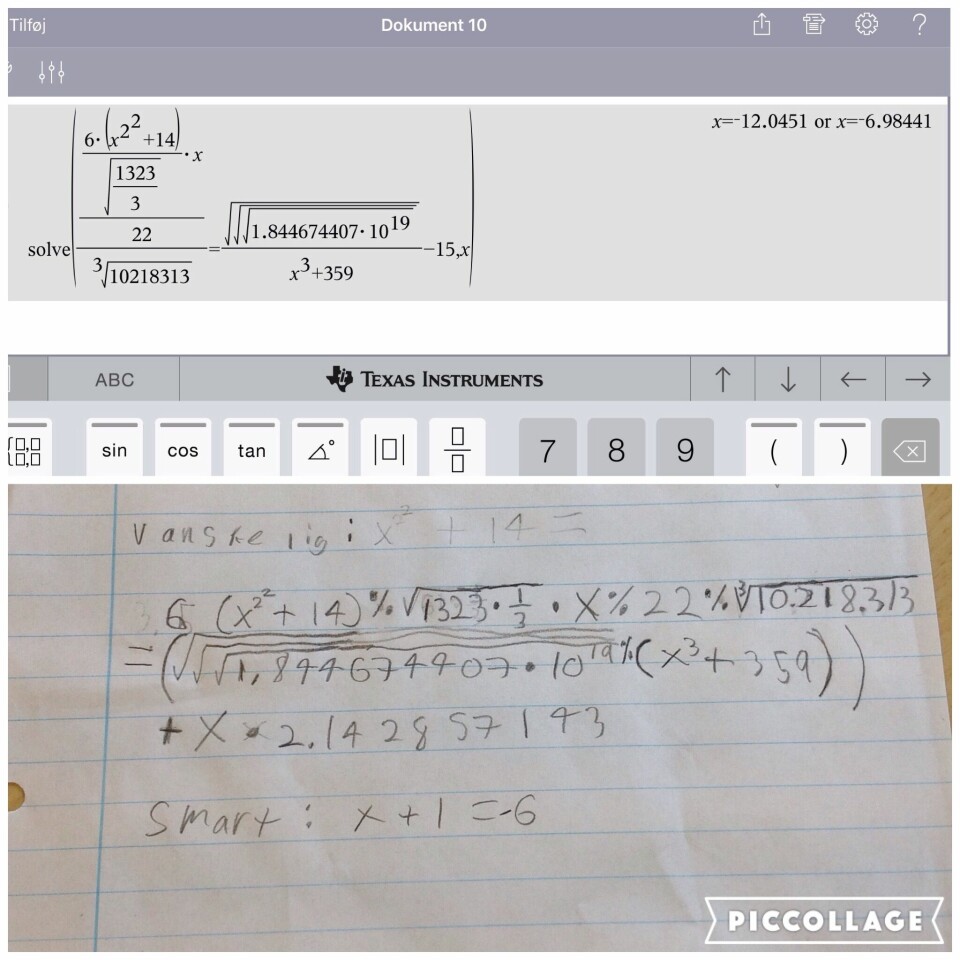
Én elev, Christian, havde uopfordret arbejdet videre hjemme med ”det vanskelige svar” på en ligning med løsningen -7. Og hold nu op en vidunderlig proces, der kom ud af det. Han strålede som en sol imens han fortalte, hvordan han havde taget udgangspunkt i at begge sider ”bare skulle give 1, fordi 1 er så nemt at regne med” og derfra givet den gas på lommeregneren, ”som på et tidspunkt viste en besked jeg aldrig har set før”.
Der var ingen tvivl om, at Christian både havde fået udfordret sig selv og sin lommeregner. Vi behandlede afslutningsvis hans ligning i et CAS-værktøj, og fik os på denne baggrund en spændende snak om to forskellige løsninger, og hvorfor det ene svar kun blev tilnærmelsesvis -7.
Min oplevelse er, at det fede ved denne åbne opgavetype er, at differentieringen ligger i selve opgaven – idet, at det vanskelige svar kun bliver så vanskeligt, som den enkelte elev gør det til! Men pointen (i dette tilfælde, at der findes et uendeligt antal ligninger med den samme løsning) kan opnås på alle niveauer. Og for første gang i laaang tid var lynhurtige Christian ikke færdig med dagens opgave efter fem minutter – ja, jeg overvejede faktisk at tjekke for livstegn efter 17 minutter med en lydløs Christian-udgave… Rent faktisk tror jeg bare Christian var i flow…. Og det samme var jeg.. både i timen og da jeg skrev dette indlæg.
Lad os åbne matematikken noget mere, og gå på jagt efter andet end blot det, der står til højre for lighedstegnet.