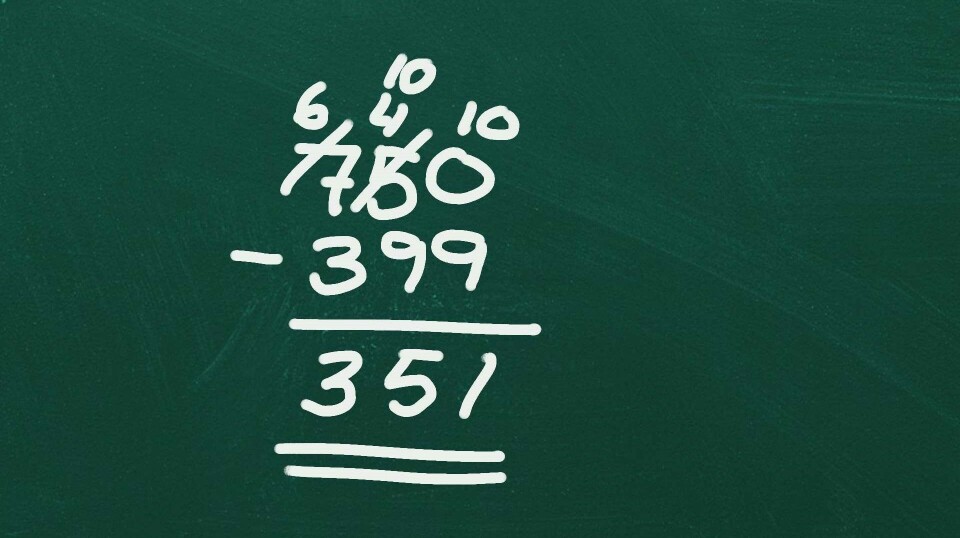Er det plus, minus, gange eller division?

Opmærksomhedspunkt i Fælles Mål

Eleverne får først mulighed for at anvende matematik, når de bliver i stand til at bringe matematikken i spil i situationer i omverdenen. For at skabe denne forbindelse mellem regning og virkeligheden arbejdes der med regnehistorier og tekstopgaver op gennem hele skoleforløbet. Det er også et opmærksomhedspunkt efter 6. klassetrin, at “Eleven kan vælge hensigtsmæssig regningsart til løsning af enkle hverdagsproblemer og opstille et simpelt regneudtryk”. I læsevejledningen for matematik uddybes det, at “Læreren må være opmærksom på, om eleven i løbet af 2. trinforløb (4.-6. klassetrin) bliver i stand til at bruge de fire regningsarter i helt enkle situationer. Det er i denne forbindelse ikke resultaterne, der er i fokus, men elevernes opstilling af et regneudtryk, der passer til situationen”.  

Synliggør matematikken

Men selvom der arbejdes med regnehistorier både i indskolingen og på mellemtrinnet, så er det ikke en selvfølge, at eleverne får lært at bruge matematikken til at løse tekstopgaverne. 

Selv elever i de yngste klasser, kan sagtens løse regnehistorier som denne: “Lise er 7 år og hendes lillesøster er 4 år. Hvor mange år er Lise ældre end sin lillesøster?”. Men selvom de hurtigt kan svare, at Lise er 3 år ældre, så er det de færreste af eleverne, som ved, at det faktisk er et minusstykke, de har regnet ud. De har løst opgaven intuitivt og brugt deres sunde fornuft - højest sandsynligt ved at tælle op fra 4 til 7. Det er også en ganske fin måde at løse denne opgave på, men det ville være fantastisk, hvis svaret blev opfulgt med “fedt, nu ved vi at svaret er 3, men hvad er det egentlig for et regnestykke, som vi har regnet ud? Hvis vi skulle have løst opgaven på lommeregner, hvilket regnestykker er det så, der giver svaret på opgaven?”. 

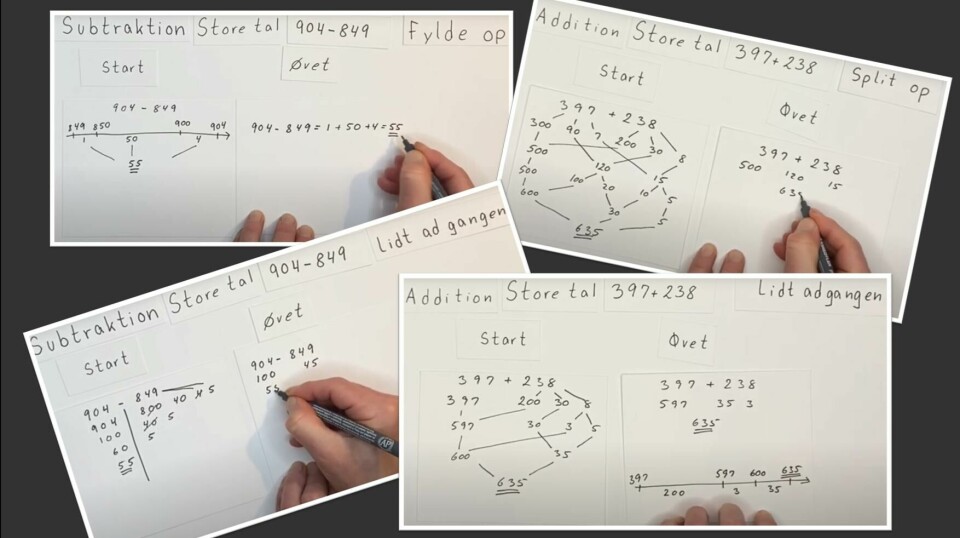
Vi er nødt til at undervise eleverne i at se koblingen mellem regnestykke og tekstopgave, mens teksterne er simple og tallene nemme, så de er i stand til at få hjælp af matematikken i deres problemløsning senere, når opgaverne og tallene bliver sværere. Det er både vigtigt, at eleverne får udvidet deres forståelse af minus til at omfatte de mange forskellige typer af situationer, som kan løses ved hjælp af minus - her var det en opgave om at finde forskellen - og samtidig at de bliver trænet i at opstille det regneudtryk, som passer til situationen. 

Arbejdet med regnehistorier er vigtigt i matematik, da de skaber forbindelse mellem regning og virkeligheden. Sørg for at hjælpe dine elever med at opdage denne forbindelse, for den kommer ikke af sig selv!