Visuelle beviser - spænder de ben for ræsonnementer?

Der findes en hel genre i matematik, proof without words. Visuelle beviser. Smukke visuelle elementer, som for en matematikglad person synes som lidt underholdning og måske en form for matematik-tegneserie. Personligt holder jeg meget af dem, fordi det giver anledning til en indre dialog om, hvorfor det er sådan og hvad der er på spil, men jeg anerkender, at der givetvis er andre, som har det anderledes med dem.

Der findes også visuelle beviser, som vi bruger i grundskolens matematikundervisning. Tænk bare på de mange arealbeviser, hvor man klipper og flytter lidt rundt, Pythagoras beviset (i den kinesiske variant, hvor man også lægger arealer op på to forskellige måder) osv. De er på den ene side smukke, fordi de så fint illustrerer den matematiske egenskab, der er på spil. På den anden side er det jo værd at overveje, om eleverne faktisk ser det indlysende på samme måde som matematiklæreren gør.

Risikerer vi nogle gange, at klippebeviserne spænder ben for elevernes udvikling af en forståelse for de egenskaber, der er på spil? Og risikerer vi, at eleverne ikke får italesat den matematik, der ligger bag, fordi vi jo bare kan se det? Skaber vi derved en tavs viden i eleverne? En viden som ikke er forankret i en dyb forståelse af de egenskaber der foldes ud i beviset, og dermed bliver en viden, som kan bruges til at regne arealer ud alene, men uden en større indsigt i sammenhænge mellem fx arealet af et kvadrat, et rektangel, et parallelogram, et trapez og en rhombe?

Vi har en opgave i at tale egenskaberne ved figurerne frem, så eleverne kommer til aktivt at bruge egenskaberne i deres argumentation. Og når vi dykker ned i klippebeviserne, så kan det måske nogle gange være værd at bruge tid på at lade eleverne argumentere for, hvorfor de egentlig er sande de beviser. Hvad viser de egentlig?

GeoGebra lader os nemt fremstille filer, der med en skyder (slider) kan trække ting rundt, og vi kan designe og arrangere tingene, så elementerne flyver pænt på plads for eleverne. Gør vi det, skal vi også bruge tid på, at eleverne forsøger at argumentere for den matematik, der er på spil.

Eleverne kan godt undersøge sig til erkendelser af matematiske egenskaber og sammenhænge ved at trække rundt i elementer i GeoGebra. Og det skal de endelig gøre. Men når det kommer til at bevise, at noget nødvendigvis er sådan, er et dynamisk eksempel, hvor vi argumenterer i stil med; "se her, når jeg trækker rundt er det altid sådan..." ikke et bevis. Eksempler kan aldrig udgøre det for et matematisk bevis. Vi kan føle os overbevist af eksemplernes magt. Men vi har ikke bevist og argumenteret for, at det altid må forholde sig sådan. Hver ting til sin tid ikke? Vi kan godt undersøge og sætte ord på egenskaber uden at skulle bevise alt hver gang. Men nogle gange kan vi forfølge at ville bevise for at slå fast, at det nu engang er ganske sikkert, at det er sådan. Vi kan øve os på matematisk argumentation. Det er ikke der aktiviteterne skal starte. Argumentationen og bevisførelsen ligger som noget af det sidste, når eleverne først har en fornemmelse for de egenskaber, der er på spil. For nogle kan det måske være en sjov motivation at forklare egenskaberne. For andre er bevisførelse en kuriositet langt op forbi de gymnasiale ungdomsuddannelser. Men det betyder ikke, at vi ikke kan lege lidt med genren også i grundskolen.

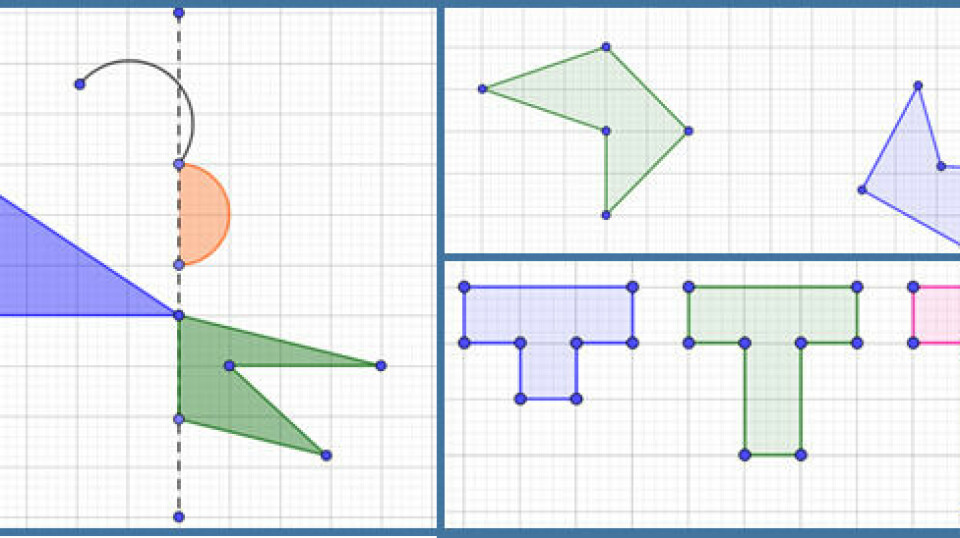
Jeg har samlet nogle eksempler på beviser fundet rundt om på GeoGebra, som spiller på det visuelle, som jeg kort beskriver herunder. Måske er det nogle, I kan bruge i undervisningen.

Vinkelsum i trekanter - eleverne kan her argumentere for, hvorfor trekanten, der drejes, lige præcis passer ind. Jeg har oversat Tim Brzezinskis fil. Tim er et utroligt produktivt menneske på GeoGebra og i det hele taget. Han har en fantastisk tilgang til matematikfaget, og der er stor inspiration at hente i hans mange filer. Det er jo også en af de fine elementer GeoGebra giver os mulighed for. Vi kan tilpasse andres fine arbejde og bruge det i vores egen undervisning. Sharing is caring!

Parallelogrammets klippebevis - eleverne kan bruge lidt tid på at argumentere for, hvorfor den retvinklede trekant, der 'klippes' af lige præcis passer ind i bunden af parallelogrammet. Her er det en fordel, hvis eleverne har styr på topvinkler og vinkler ved parallelle linjer.

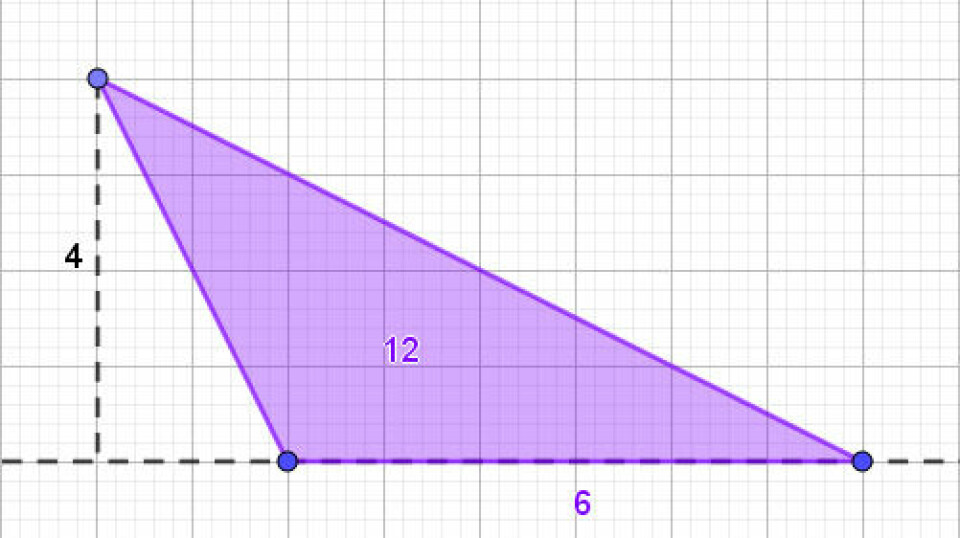
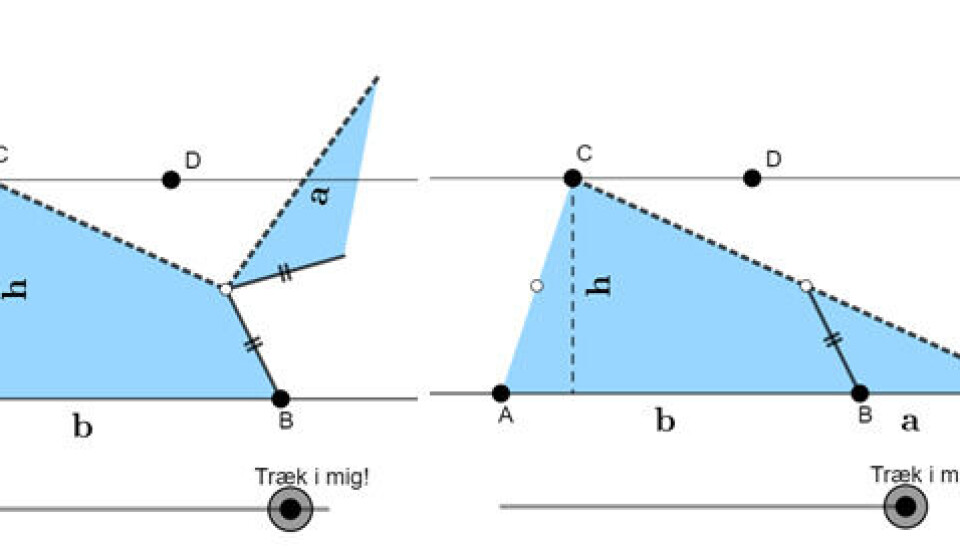
Alternativt klippebevis for trapez - eleverne kan her bruge en del tid på at undersøge, hvorfor den trekant, der klippes af lige præcis passer ved siden af. Og hvorfor trapezformlen egentlig minder om arealformlen for en trekant. Det er et alternativ til det mere klassiske bevis, hvor man bare drejer trapezet om sig selv og dermed får to i forlængelse af hinanden. I dette bevis er der god mulighed for at folde vinkler ved parallelle linjer ud i flere sammenhænge, samt topvinkler.

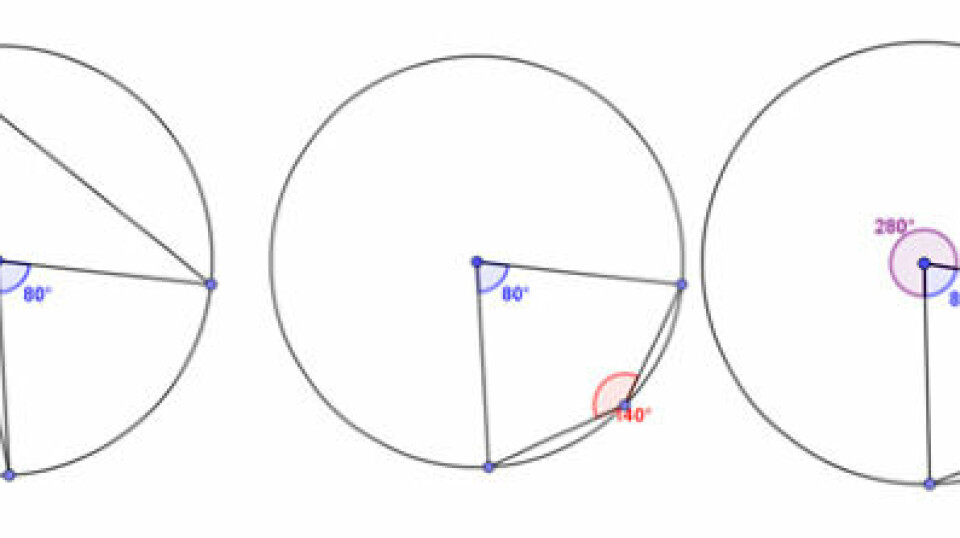
Visuelt bevis for periferivinkel og centervinkel - eleverne kan sagtens undersøge sig til en erkendelse af, at en periferivinkel er det halve af den centervinkel, den spænder over. Men det at erkende ,at det er sådan ved at trække rundt på en cirkel i GeoGebra er jo ikke det samme som at have bevist, at det nødvendigvis er sådan. Vi skal ikke starte med beviset, vi skal starte med undersøgelsen. Dette eksempel er et særtilfælde, hvor det ene vinkelben går gennem radius, og altså udgør en diameter i cirklen. Det gør beviset lidt enklere. Men man kan selvfølgelig påpege, at det er et særtilfælde. Der er dog ikke langt fra at have argumenteret for dette bevis til at have argumenteret for det generelle - som der også ligger utallige eksempler på inde på geogebra.org.

Arealet af en cirkel - her kan eleverne arbejde med klippebeviset for en cirkels areal. Anthony Or, som har lavet denne fil har så mange flotte filer, at hans profil på GeoGebra bestemt er et besøg værd.

Hvad kan vi gøre konkret? Eleverne kan skærmoptage forklaringer af beviserne, eller de kan skrive små forklaringer til, måske som en tegneserie, hvor de tager skærmbilleder undervejs og tegner og beskriver til hvert skærmbillede.

Hvordan bruger du visuelle beviser med dine elever? Del gerne dine erfaringer på bloggen.