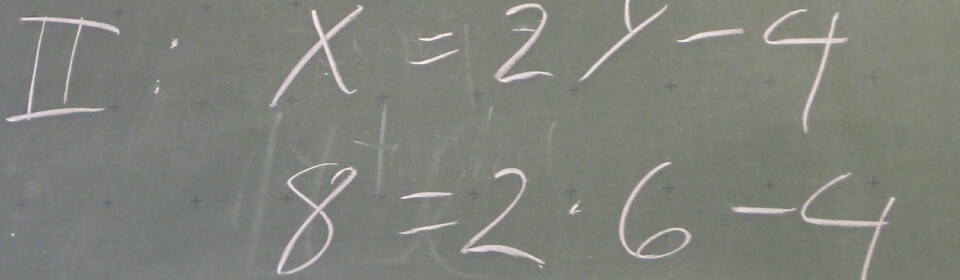
Matematikkonsulenternes blog
Blog
Hvor ofte bruger du dynamiske konstruktioner i din matematikundervisning?
Dynamiske konstruktioner kan være en gave til at skabe undren og forstyrrelse hos eleverne. Og i de situationer, er der måske god basis for læring.
Når vi konstruerer eller tegner figurer på papir med blyant og tegneredskaber, bliver konstruktionen statisk. Vi kan ikke ændre på den efterfølgende, med mindre vi bruger viskelæder, og så er det ofte forfra med mange af tingene. I dynamiske geometriprogrammer som GeoGebra er det ofte nemt at justere på en tegning eller en konstruktion, man kan bare flytte punkter, og så følger tingene som regel med.
Man kan diskutere, om tegning og konstruktion er det samme. Jeg tænker, at der er en væsensforskel mellem de to, da tegninger i min forståelse ikke behøver have rigtige mål eller forhold, men en konstruktion bygger på nogle bestemte forhold og mål. Man kan selvfølgelig sige, at en præcis tegning gør det samme, men så hedder den også noget andet end bare en tegning.
Til sagen. Det jeg vil diskutere med jer i dagens blogindlæg er, hvorvidt vi arbejder statisk eller dynamisk, når vi tegner eller konstruerer i GeoGebra?
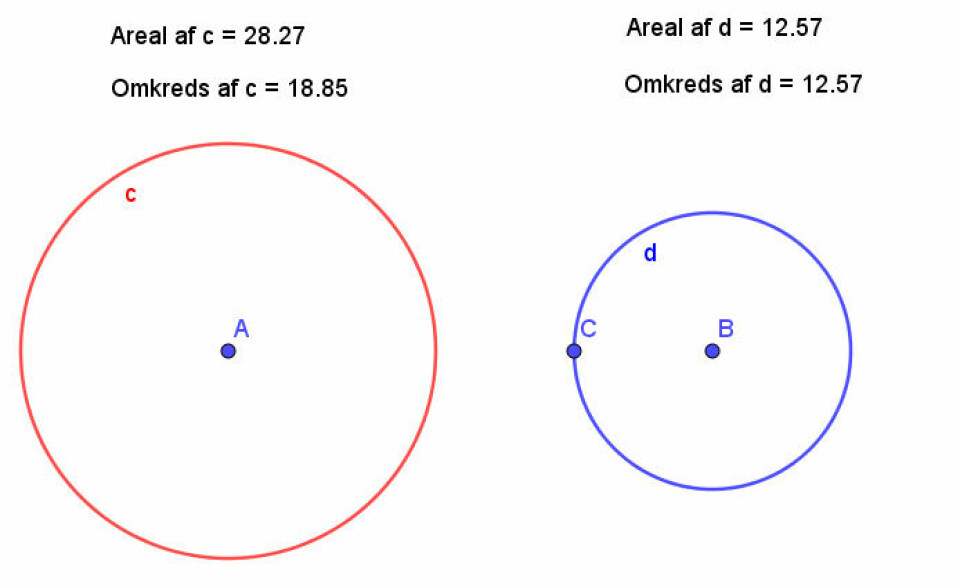
Som et lille tænkt eksempel, kan jeg konstruere en cirkel med radius 3. Jeg kan da efterfølgende ikke gøre så meget med min cirkel, da den altid vil have radius 3. Jeg kan måle areal og omkreds, men konstruktionen i sig selv er temmelig kedelig i udgangspunktet. Hvis jeg i stedet bare tegner en cirkel med en variabel radius, altså bare et linjestykke, jeg kan justere længden på, får jeg pludselig noget, der er dynamisk. Jeg kan nu undersøge hvordan areal og omkreds udvikler sig, når jeg justerer på radius. Jeg kan undersøge, om areal og omkreds kan have samme værdi osv. osv. Selve konstruktionen af cirklen var der jo ikke det store i. Men de spørgsmål, vi kan stille til eleverne, når de arbejder i dynamiske geometriprogrammer bliver meget mere mangfoldige, når vi stiller dem ud fra dynamiske konstruktioner. Og ofte er eleverne nødt til at forholde sig til noget de ser ske på skærmen, og tænke over det i stedet for blot at gå efter bestemte tal/resultater. Hvad sker der med x, når jeg ændrer på y? Den slags overvejelser trækker måske på mere end en instrumentel forståelse af begreberne. Findes der mon andre værdier, hvor areal og omkreds kan få samme værdi på den blå cirkel? Hvorfor/hvorfor ikke? Det kan indskolingselever godt observere på og komme med bud på, selvom de ikke kender til pi og areal- eller omkredsformler for cirklen. Og det giver dem indblik i nogle grundlæggende egenskaber ved cirklen som figur.
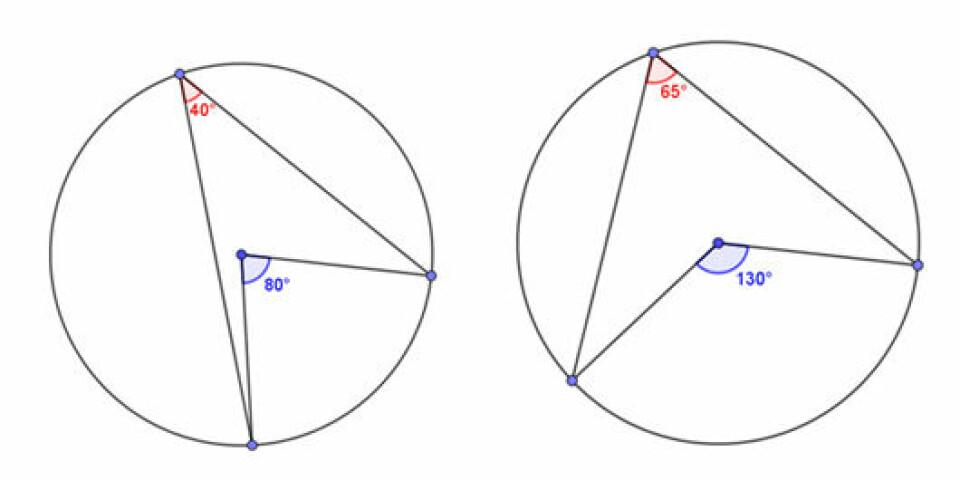
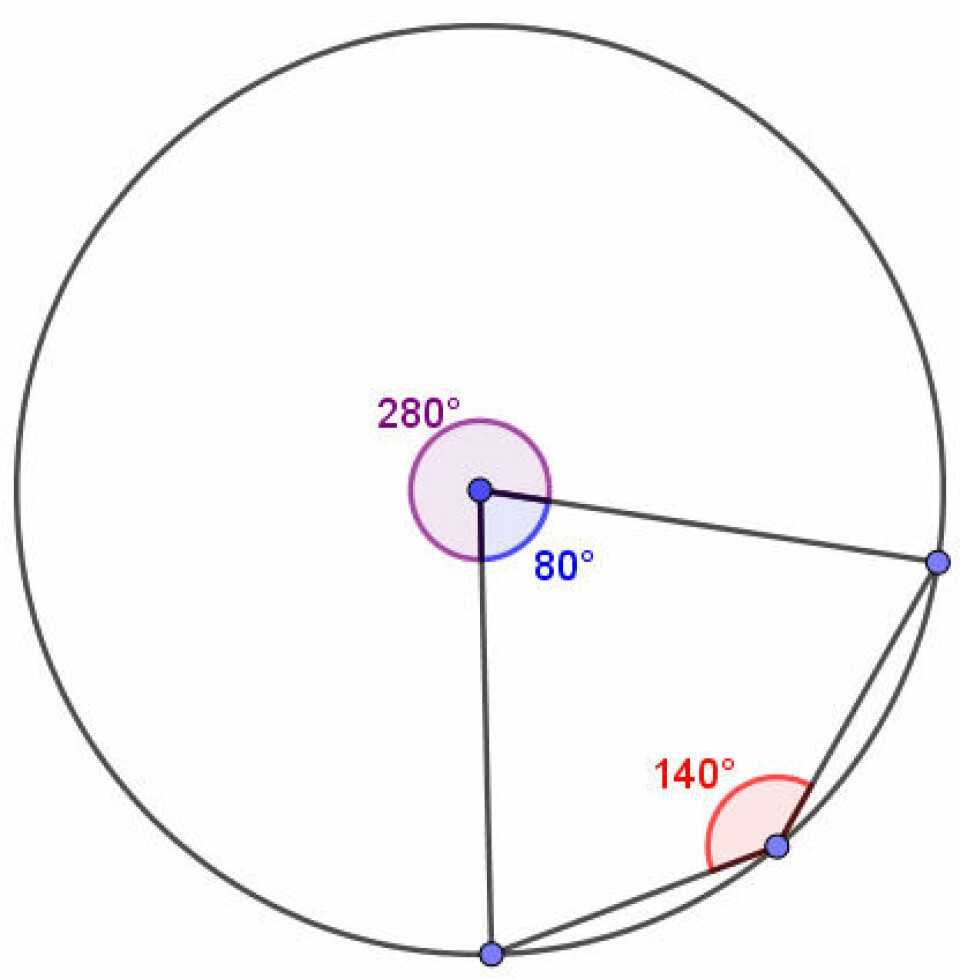
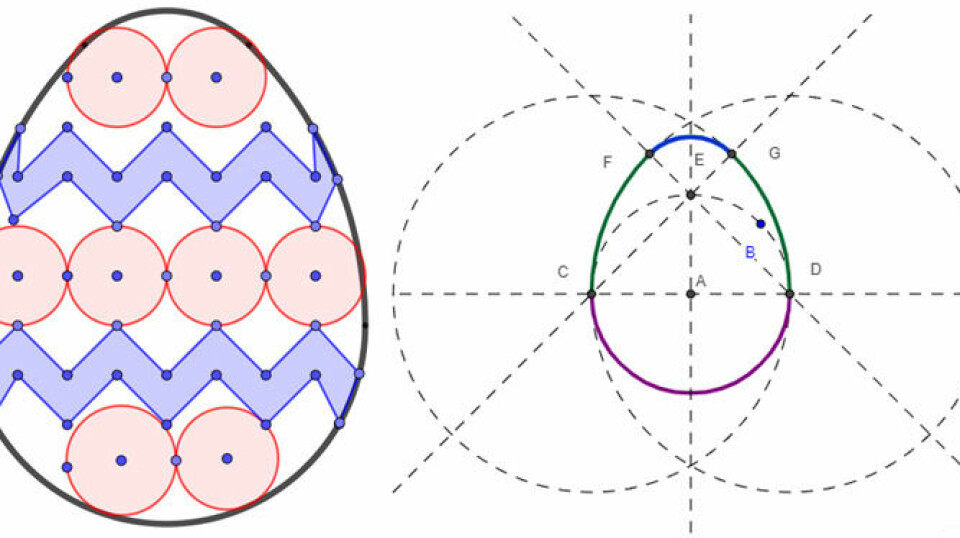
Spoler vi lidt frem i skoleforløbet, kunne det være, at man arbejdede med centervinkler og periferivinkler. Her er det overordentlig meningsfuldt at arbejde med dynamiske konstruktioner. Hvis vi konstruerer en cirkel (radius er uden betydning, men cirklen skal helst ikke ændres i størrelse her), og lægger tre punkter på cirklen kan vi konstruere en periferivinkel og centervinklen med udgangspunkt i cirklens centrum.
For selv det utrænede øje, vil den åbenlyse sammenhæng mellem de to vinkler være til at få øje på. Især hvis man her udnytter det dynamiske og lader eleverne trække lidt rundt i punkterne. Igen er det de gode spørgsmål, som lægger op til at eleverne skal forholde sig til det, de ser på skærmen, der er afgørende.
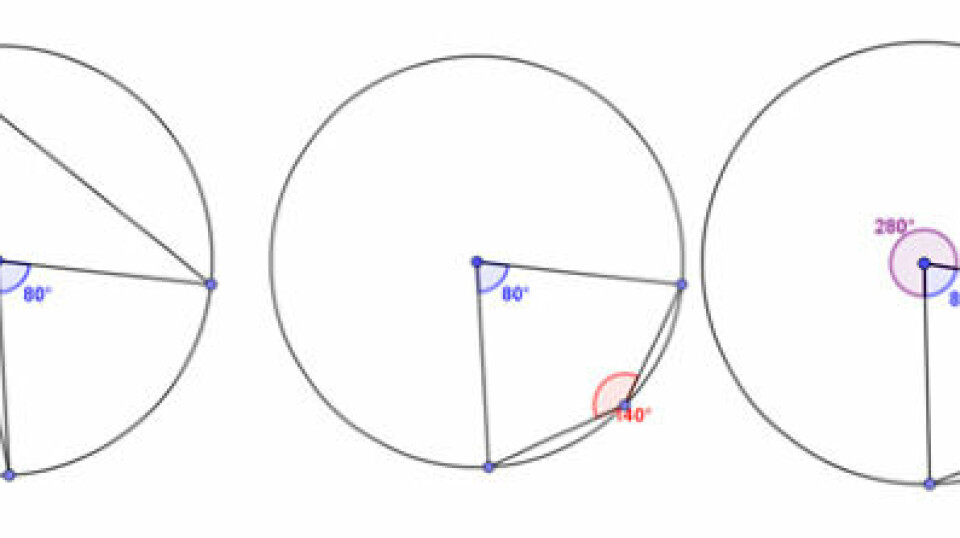
Hvilken sammenhæng kan du få øje på mellem den røde og den blå vinkel? Kan du finde situationer, hvor det ikke gælder ved at flytte på de blå punkter? Find mindst tre eksempler, som kan være interessante for klassen at diskutere.
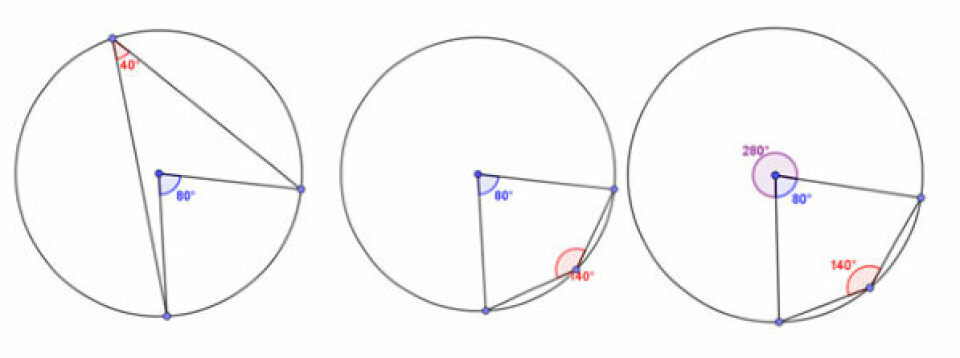
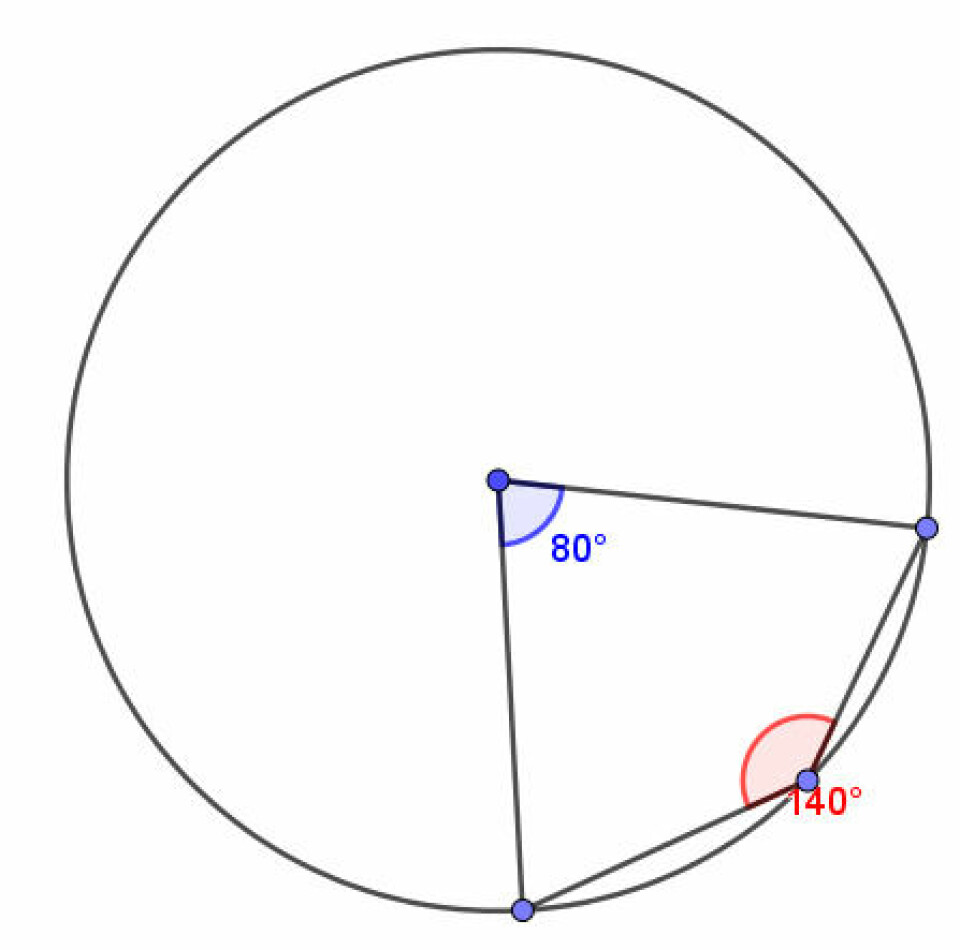
Mit bud er, at det vil eleverne godt kunne komme til at finde situationer, hvor deres første indlysende regel møder modstand, nemlig, hvis de trækker punktet med periferivinklen om på modsatte side af cirklen i forhold til de to illustrationer herover. Periferivinklen på min konstruktion er indstillet til altid at vælge værdien mellem 0 og 180 grader. Og dette tilfælde er jo faktisk en gave. For hov - gælder reglen nu ikke? Er det faktisk omvendt nu?
Men hvad er så egentlig en periferivinkel og en centervinkel? Måske vi må ty til et opslagsværk (det står desværre ikke i Matematiske formler og fagord).
Hans Jørgen Beck skriver på s. 126 i Gyldendals små opslagsbøger - Matematik (2009), at;
”En periferivinkel er en vinkel, der har vinkelspidsen på et punkt af en cirkelperiferi, og hvis ben skærer periferien i to andre punkter.
De to vinkelben vil afskære en bue på cirkelperiferien. Om periferivinklens størrelse gælder:
En periferivinkel er halvt så stor som den bue, den afskærer.”
I bogen findes også en fin illustration, som viser, hvad der menes med buen.
Det kan give anledning til en ret fantastisk snak om, hvad er det egentlig for en bue, den periferivinkel afskærer? Og eleverne kan få øje på, at det faktisk er vinklen på den modsatte side, som skal i spil her. Det kan igen give anledning til at måle begge centervinkler og i hvert tilfælde vurdere, hvilke centervinkel er det, som dækker over samme bue, som periferivinklen. Og så kan vi næsten ånde lettede op igen, for nu ser det ud til, at vores regel faktisk passer igen.
Der findes masser af eksempler på aktiviteter fra fx geometriens verden, som egner sig utrolig godt til at blive arbejdet med i et dynamisk setup, hvor man kan støde på forstyrrelser undervejs, som giver anledning til, at elevernes forståelse af og billeder på begreberne bliver udfordret, udviklet og forfinet. Og måske kan vi ved at arbejde på den måde, sætte fokus på den der forståelse, som sigter mod noget andet, end blot at regne den ud.
Går du selv rundt med vilde fede dynamiske ideer, så vil jeg opfordre til, at du deler dem i kommentarfeltet her, eller med en god kollega, så vi kan få dem ud til endnu flere af vores gode matematikkolleger over hele landet.
Tak fordi du læste med i dag.