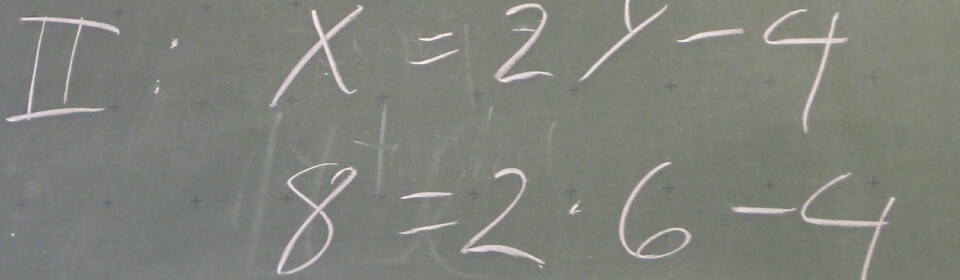
Matematikkonsulenternes blog
Blog
Hvordan kan vi få eleverne til at tænke mere og ikke mindre med GeoGebra?
Hvilke gode opgaver og hvilke smarte didaktiske greb kan vi bruge i matematikundervisningen, som fremmer mere tænkning og rummer potentiale for udvikling af matematisk forståelse?
Mange digitale værktøjer i matematikundervisningen kan udføre beregninger og løse opgaver inden for forskellige områder af matematikken hurtigere og ofte mere præcist, end vi kan med vores egen hjernes processorkraft. Lommeregneren og de forskellige digitale værktøjer kan på en måde blive tryllestave, vi svinger, hvorefter svaret på magisk vis dukker op foran os. Således kan vi på bedste Harry Potter vis fikse problemer og løse udfordringer ofte uden at tænke over, hvad der egentlig sker i maskinen. Vi udliciterer løsningen af opgaven til maskinen og afkobler langt hen ad vejen vores egen matematiske tænkning.
Der er utrolig mange elementer i programmer som GeoGebra, man kan begejstres over, fordi det er sådan et stærkt visualiseringsværktøj i forhold til matematikken. Det er også stærkt til at beregne og give eleverne en masse her og nu resultater, uden at de selv behøver regne.
Jeg vil dog med dette blogindlæg slå et slag for, at vi også bruger programmet til at sætte eleverne i situationer, hvor de skal tænke mere over matematikken og ikke bare få en masse svar og data foræret. Et af de primære formål med matematikundervisningen, og dermed også med inddragelsen af programmer som GeoGebra i undervisningen, er netop at udvikle elevernes forståelse af matematikken. Det kræver, at vi forstår at udnytte maskinens enorme beregningskraft og visualiseringsmuligheder til at undersøge matematikken. Det kræver dog samtidig, at vi grundigt overvejer, hvordan vi stiller spørgsmål og opstiller problemer i matematik, så det bliver meningsfuldt at inddrage de digitale hjælpemidler.
Problemstillingen er ikke en, der diskuteres særlig tit i de matematikfora, hvor matematiklærere mødes for at sparre om faget. Her er der oftere fokus på teknisk tastehjælp og lister over, hvilke værktøjer man skal kunne bruge i programmerne, når emnet er de digitale hjælpemidler.
Derfor vil jeg gerne give bolden op for et nyt fokus i diskussionen om de digitale hjælpemidler. Det er mit håb, at vi sammen kan udvikle gode opgaver og gode didaktiske greb, så vi får sat eleverne i situationer, hvor de netop skal tænke mere over matematikken støttet af de digitale hjælpemidler.
Jeg har tre bud herunder, og jeg håber, at I vil bidrage med jeres bud også.
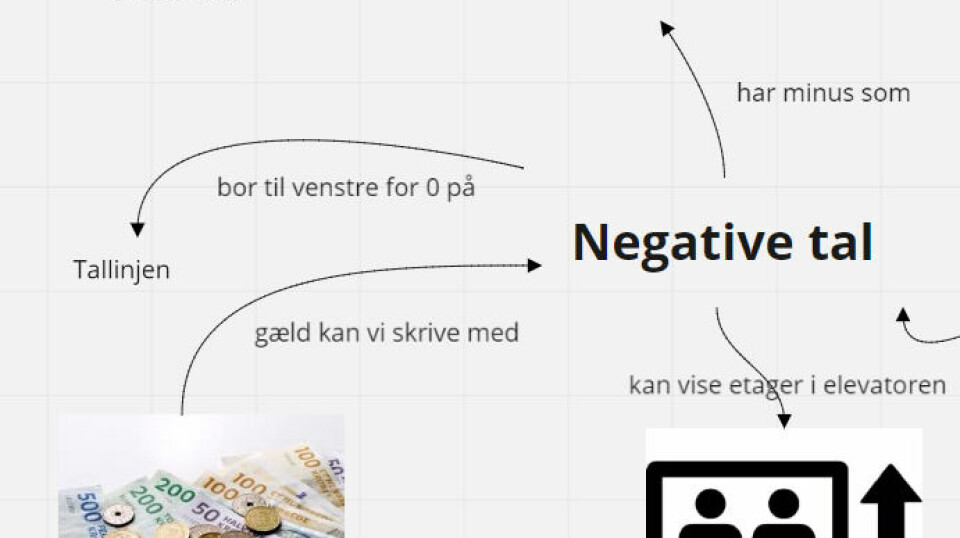
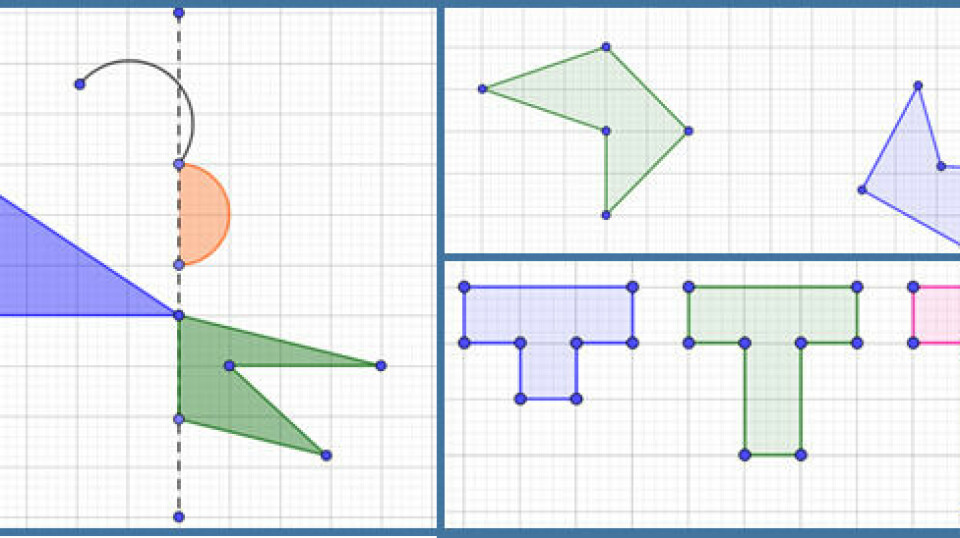
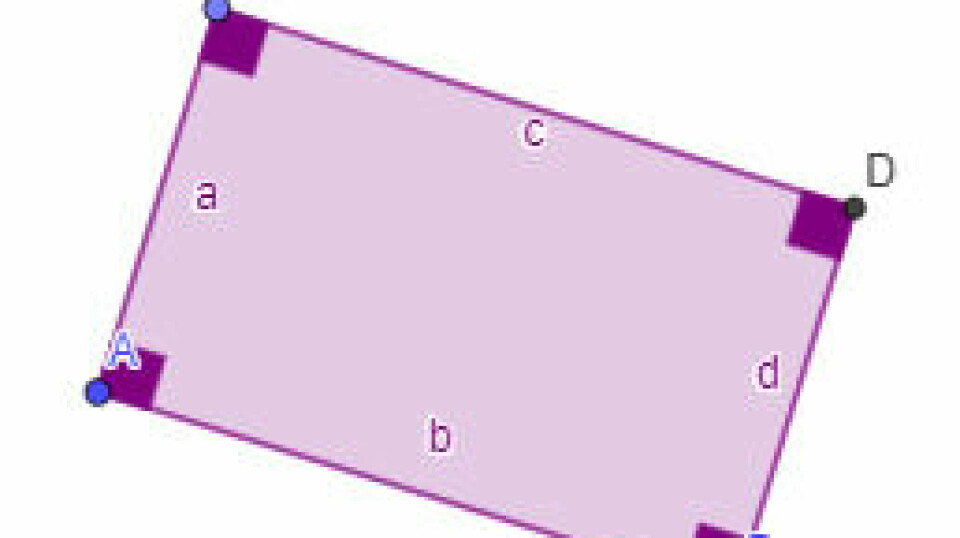
- Omsæt forklaringen til figur, graf, datasæt mm. Opgaver, hvor der er givet en sproglig forklaring af en figur, en graf, et datasæt eller lign. Eleverne skal kunne omsætte det sproglige til noget konkret. De skal skifte fra en repræsentationsform til en anden, og det kræver i den grad, at de tænker mere og ikke mindre. Det kan være en støtte at arbejde i GeoGebra i stedet for at tegne i hånden, da det er nemmere at rette eller justere til undervejs. Det er en god måde at få begreber i spil på, og få fokus på forståelsen af centrale begreber, fx spids, ret, stump vinkel, netop osv. Der er et eksempel på sproglige forklaringer af trekanter og firkanter her.
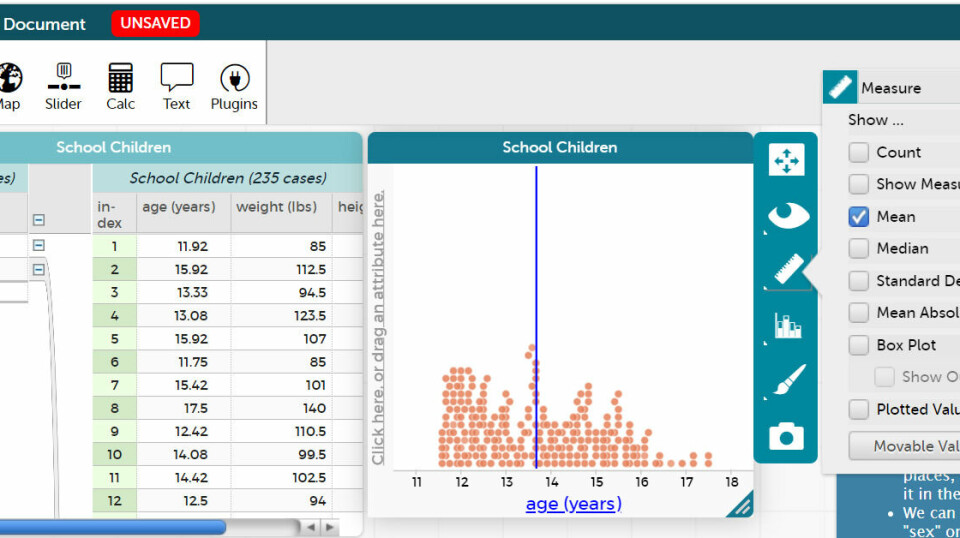
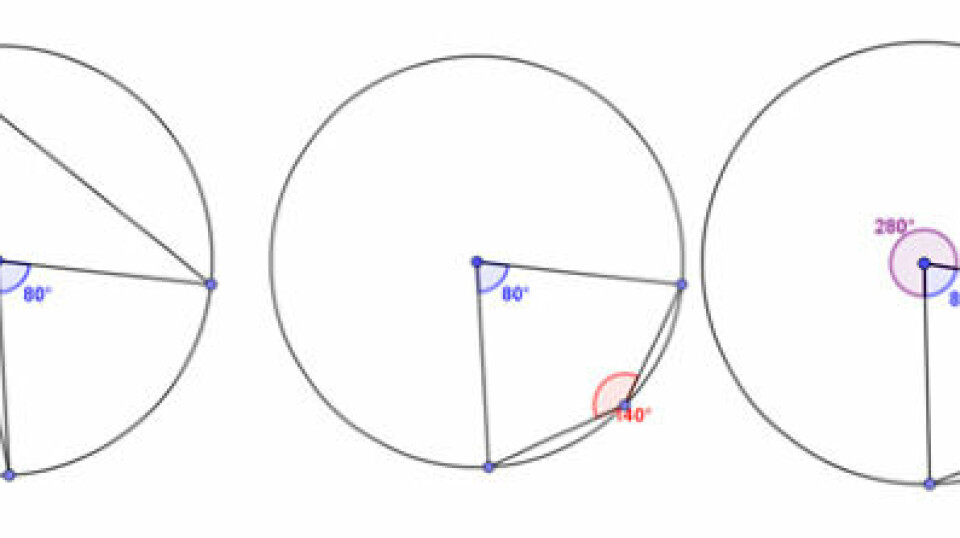
- Undersøgende arbejde med at finde systemer/mønstre i forskellige fænomener i matmatikken. Eleverne kan fx undersøge forskellige lineære forskrifter særligt udvalgt af læreren. Det gøres ved at tegne graferne og se sammenhængen mellem den visuelle repræsentation (graf) og den symbolske (forskrift). Undersøgelsen kan understøttes med spørgsmål om, hvad nogle bestemte grafer har til fælles i hhv den visuelle og symbolske repræsentation? Her kan man få eleverne til at få blik for hældningstal og skæring med y-aksen. Man kan desuden bede elever om at justere i forskrifterne og forholde sig til, hvordan det påvirker graferne. Som næste trin kan man lade eleverne komme med forudsigelser om, hvad der skal til af justeringer af forskriften for at der fremkommer en graf med bestemte egenskaber (hældning, placering, gå gennem bestemte punkter, mm). Til slut kan eleverne formulere generelle regler for sammenhængen mellem forskrift og graf. Se eksemplet her. Andre eksempler kunne være undersøgelser af: - betydningen af toppunktets placering for rumfanget i en pyramide. - sammenhængen mellem forskellige typer rumlige figurer med samme grundflade. - vinkelsummen i mangekanter. - sammenhængen mellem radius og Pi. - visuelle beviser for Pythagoras’ læresætning. - variables betydning i et regneudtryk vha skydevariable. - visuelle beviser for kvadratsætningerne.
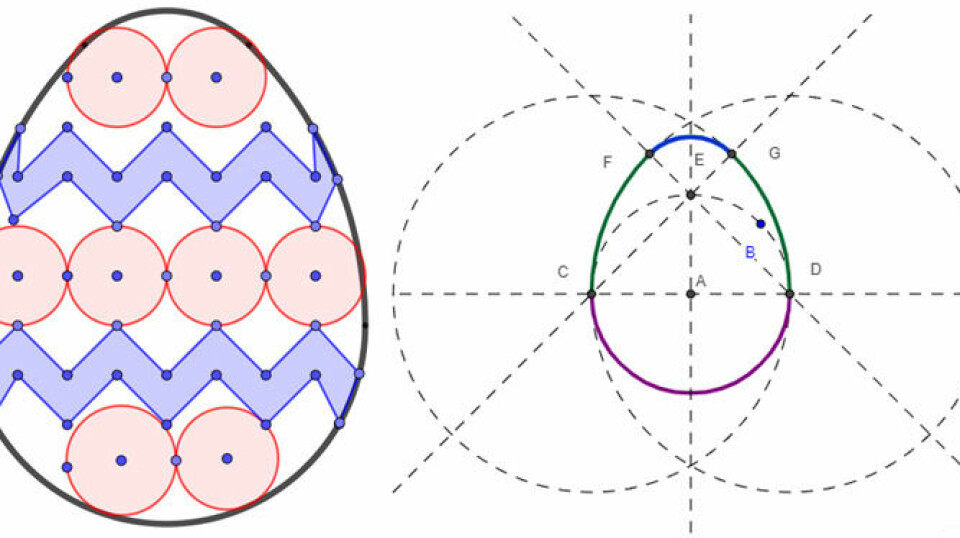
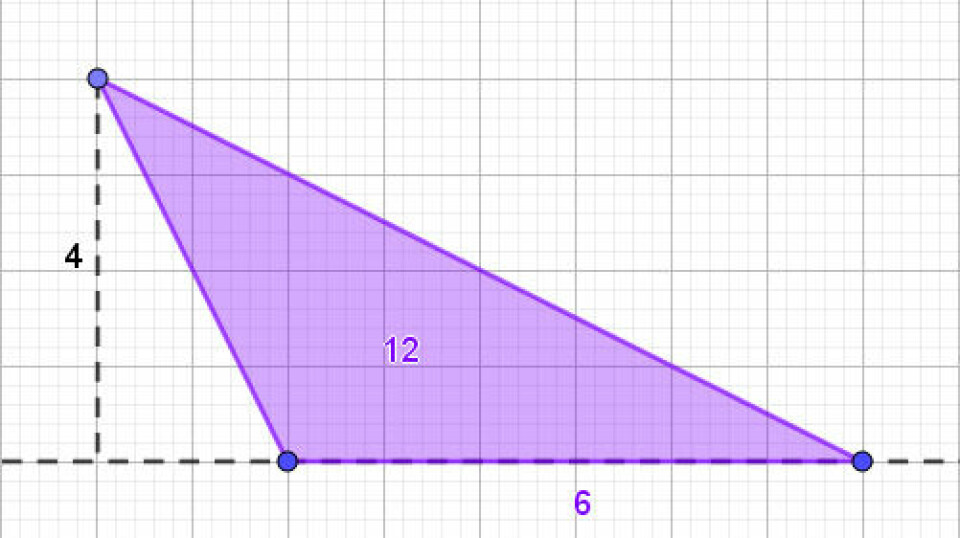
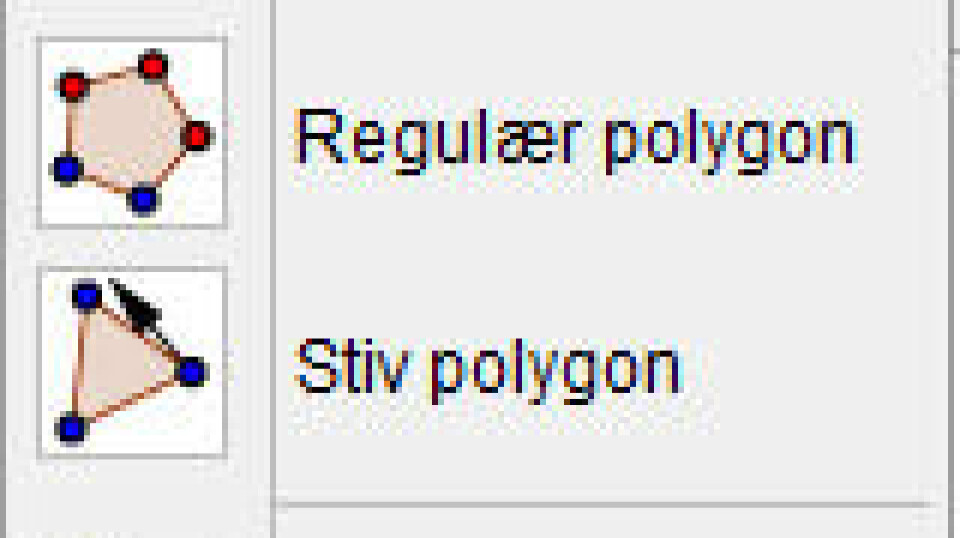
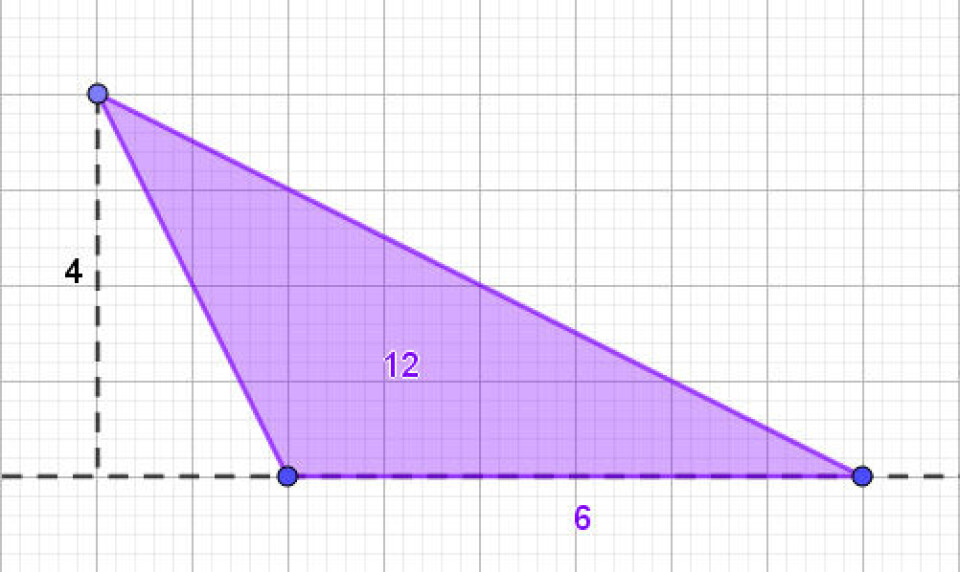
- Konstruere ’omvendt’. Hvis man fx skal konstruere en trekant, hvor arealet altid er 12 uanset, hvordan vi trækker i trekanten, hvordan skal trekanten så konstrueres? Her skal eleverne have en forståelse af, hvilke faktorer, der påvirker trekantens areal, og arealformlen kommer så at sige i spil i en omvendt form. Her må man tænke i grundlinje og højde, hvordan man overhovedet får tegnet en højde, når trekanten skal være dynamisk? De fleste elever kan arbejde i specialtilfælde, fx med grundlinje 6 og højde 4, og så konstruere konkret derudfra. Det er en oplagt mulighed til at få arbejdet med nogle gode konstruktionsteknikker, som jer, der kender mig, også ved, jeg er stor tilhænger af. Man kan også konstruere sin fil helt dynamisk, så højden tilpasser sig grundlinjen, det kan I set et eksempel på her. Filen kan også være udgangspunkt for et analysearbejde ud fra spørgsmålet ”Hvordan virker filen?”. Eleverne kan både svare i hverdagssprog, men beregninger og skitser, eller ved at genskabe filen fra bunden. I det sidste tilfælde er det primært afprøvningen af den dynamiske konstruktion, der får eleverne til at tænke mere.
Jeg håber, indlægget har inspireret til en anden vinkel på samtalen om digitale hjælpemidler i matematikundervisningen, og at det er et tema I vil tage op i fagteamet, i efteruddannelsesregi og i diverse fora for matematikundervisere.