Makkeropgaver i GeoGebra.

Vi kan bruge et digitalt værktøj som GeoGebra på forskellige måder i undervisningen, og afhængigt af vores valg kan værktøjet komme til at indtage forskellige roller i matematikundervisningen.

Vi har tidligere skrevet om at få eleverne til at tænke mere og ikke mindre med GeoGebra. I dette blogindlæg vil vi komme med nogle ideer til at bruge programmet, så det understøtter et flerstemmigt klasserum.

Når eleverne konstruerer, tegner, opretter grafer eller andet i GeoGebra, er det ofte en proces mellem eleven og skærmen. Men måske kan vi i den måde, hvorpå vi introducerer aktiviteten, skabe rum for, at eleverne i højere grad involveres i hinandens processer. Vi kan fx lægge op til samskabelse ved, at eleverne i fællesskab udvikler produkter enten synkront eller asynkront. Et andet greb er at lade eleverne forholde sig til hinandens løsninger og produkter. På den måde kan eleverne spejle sig i hinandens tanker, og de forskellige løsninger kan være udgangspunkt for en forhandling af mening om og forståelse af matematikken. Måske havde de forventet andre løsninger end de, der er fremkommet. Kan begge dele være rigtige så? Og hvorfor? Er der forskellige veje til målet, og er nolge veje mere hensigtsmæssige end andre? Det kan også ske, at eleverne må erkende, at de ikke kan løse opgaverne. Det kan føre til en diskussion om hvorvidt det skyldes, at de er for svære, eller at de faktisk ikke kan løses, fordi opgavestilleren har overset noget? Igen kan der være basis for gode drøftelser, og det kan være en god øvelse at argumentere for, hvorfor en opgave ikke kan løses.

Uanset om man er fysisk sammen i klassen eller arbejder i fjernundervisningen online, gælder det stadig om at skabe rum for dialog mellem eleverne. 

Lad os se på et par eksempler.

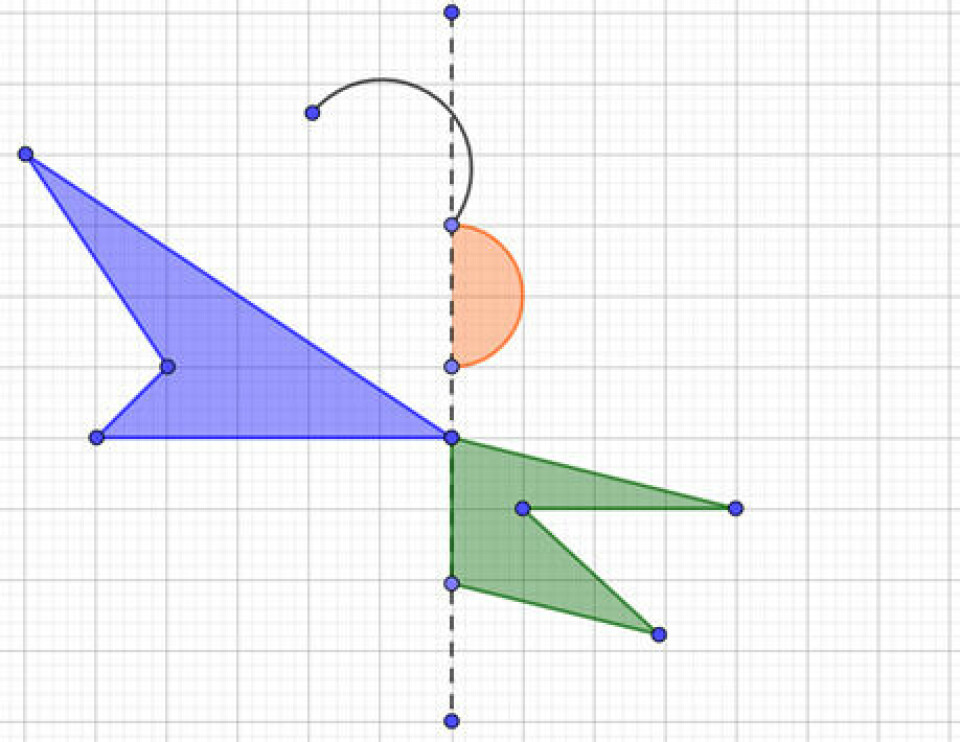
Spejling til din makker (indskolingen)

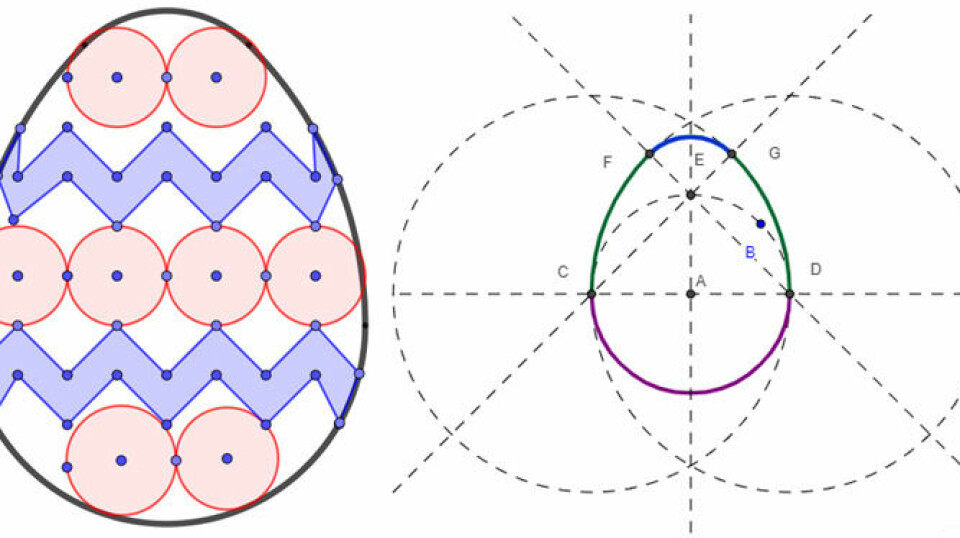
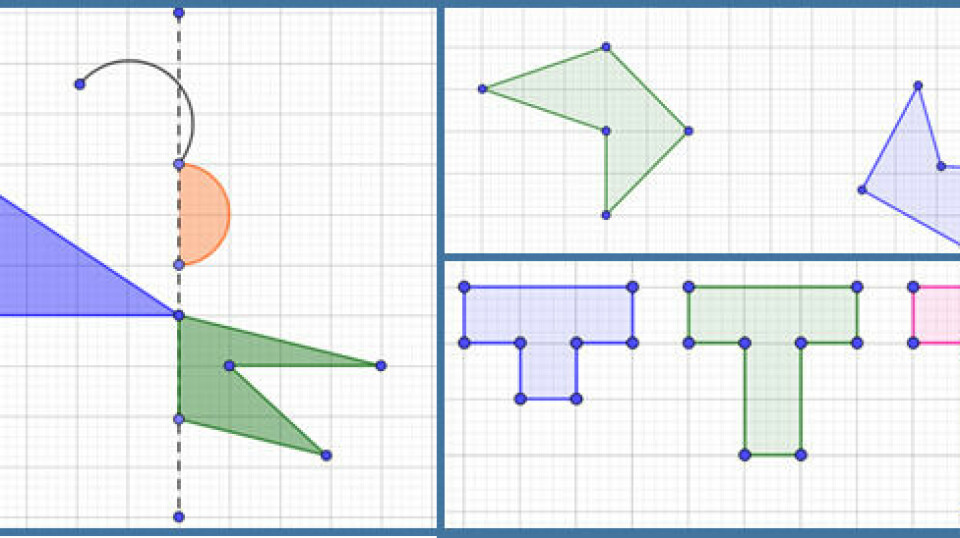
Lad eleverne fremstille halvdelen af en figur, som makkeren skal tegne færdig ved at spejle. Man kan enten lægge op til, at de skal tegne på den ene side af spejlingslinjen, eller de kan, som herunder, tegne på begge sider af spejlingslinjen. Man kan også arbejde med to spejlingslinjer, så eleverne fremstiller en fjerdel af et mønster med symmetri, som makkeren skal tegne færdigt ved at spejle.

For eleverne kan det være motiverende at skulle fremstille noget matematik, som andre skal løse. Det kan også være en måde at arbejde bag om stoffet på. Får de tegnet noget, som kan spejles af andre og kommer det til at se ud, som de havde tænkt det? Hvis ikke, hvad kan så være gået galt, og har de undervejs været opmærksomme på, om mønsteret har en tilpas sværhedsgrad? Disse refleksionsspørgsmål skal finde ved i undervisningen via samtale.

Aktiviteten kan bruges både i indskolingen, men også på mellemtrinnet eller hvor man i øvrigt arbejder med flytninger.

Gæt min flytning (hele skoleforløbet).

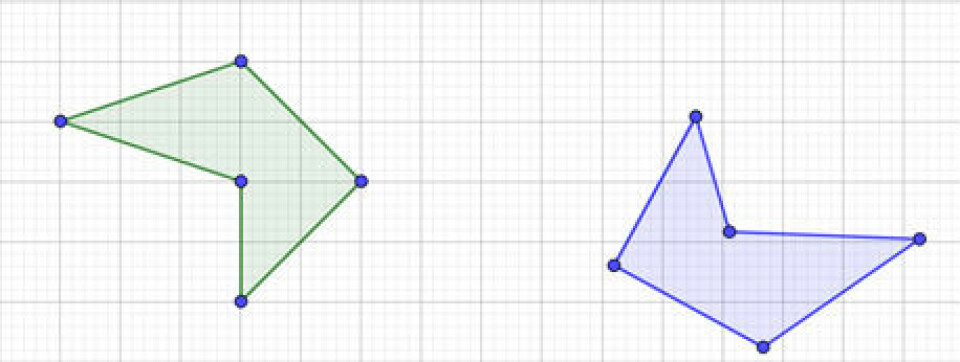
Eleverne skal her oprette en figur og flytte den ud fra aftalte flytninger, fx spejling, parallelforskydning og drejning (vælg pæne rotationer - fx 45 grader, 90 grader osv.).

Eleverne kan vælge en enkelt flytning (indskoling/mellemtrin) eller de kan udføre en sammensat flytning (mellemtrin/udskoling). Vær dog opmærksom på, at en sammensat flytning hurtigt bliver kompleks, og der derfor er brug for regler om at bruge gitterpunkter, pæne tal og et loft på antallet af flytninger. Eleven opretter sin eller sine flytninger og skjuler mellemstationer, spejlingslinjer, punkter der er drejet om osv. Makkeren modtager nu en opgave, hvor der er en original figur og den flyttede slutfigur. Makkeren skal nu være flytningsdetektiv og identificere, hvilke flytninger, der kan være foretaget.

Ofte vil eleverne erfare, at der er mange rigtige måder at flytte figurerne på, så de lander samme sted. Nogle kan endda udvikle en flytningsstrategi - parallelforskyd et punkt på plads og klar resten med spejling.

I arbejdet med denne aktivitet oplever vi ofte nogle indledende frustrationer, men vi oplever også, at de hurtigt går over i samtaler om måder at flytte på, mens eleverne sidder og peger ivrigt ind på skærmen. Oftest er omdrejningspunktet for diskussionerne enten et mislykkedes forsøg på at få figuren på plads, hvor ”gætteren” har behov for at se, at det kan lade sig gøre. Ellers handler de tit om, at ”opfinder” og ”gætter” har brugt forskellige strategier og er optagede af, hvordan den anden part har gjort. Den slags diskussioner har vi ikke tidligere set i arbejdet med flytninger, og det ender tit i matematiske samtaler om regler og definitioner i forbindelse med de forskellige flytninger.

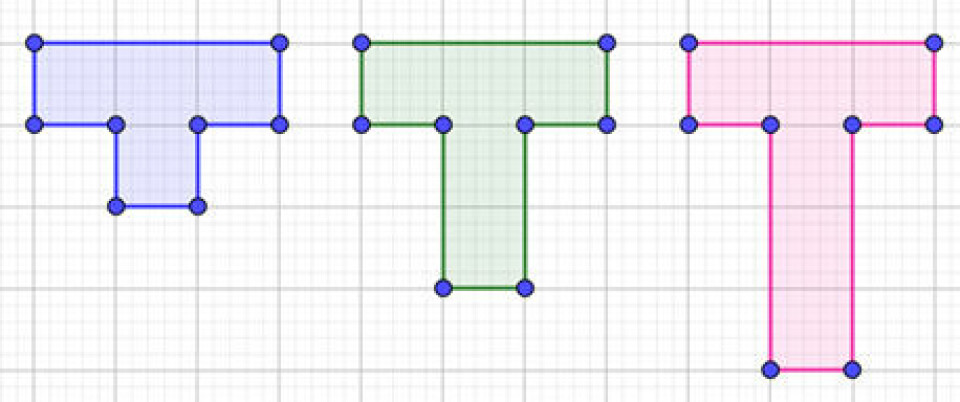
Figurfølger til din makker (hele skoleforløbet).

Når man arbejder med figurfølger, er det oplagt, at eleverne fremstiller deres egne figurfølger. Eleverne kan tegne de tre første trin af deres selvopfundne figurfølge i GeoGebra, og makkeren skal så tegne de næste to.

Alt efter hvilket trin man er på, kan man tilføje flere lag her. Fx kan makkeren skulle oversætte figurfølgen til en tabel, en graf, en funktionsforskrift osv.

Nogle gange vil eleverne opleve, at der kan være flere mulige tolkninger af en figurfølge, og det kan give anledning til gode drøftelser om, hvad der vokser, og hvordan vi kan se systemet.

Der findes helt sikkert masser andre gode eksempler på, hvordan man kan få eleverne til at lave makkeropgaver til hinanden, så de enten samskaber, får mulighed for at bruge deres viden aktivt sammen, eller får mulighed for at skulle sætte sig ind i hinandens tænkning og tolkning af matematikken.

Måske vil du dele nogle af dine erfaringer i kommentarsporet herunder? Eller med en kær kollega?