Digitale værktøjer i prøverne i matematik

Vi bringer ikke løsninger i blogindlægget, da prøverne jo bliver brugt af mange af jer i undervisningen, og det vil vi ikke ødelægge mulighederne for ved at bringe facit her. Vi vil altså udelukkende bringe nogle perspektiver frem på, hvordan GeoGebra kunne bruges - eller ikke bruges i opgaverne. 

Er en skitse i hånden det hurtigste?

I FP9 er opgave 3 en 1-spørgsmålsopgave, som handler om at undersøge, hvor mange flyttekasser med bestemte mål, der kan blive plads til i en trailer. Opgaven er en undersøgelse, og eleverne skal undersøge, hvor mange flyttekasser, der højst kan være i traileren. De skal begrunde deres svar med beregning og skitser, der viser, hvordan kasserne kan placeres.

Vi hæfter os ved beregning og skitser. For nogle elever vil en skitse her være en hurtig håndtegning med mål. For andre føles det måske tryggere at tegne fx i dynamisk geometri for det er jo mere præcist. Opgaven kan hurtigt blive meget tidskrævende, hvis man giver sig til at tegne i et dynamisk geometriprogram - eller endda kaster sig ud i at tegne i et 3d-tegneprogram. Det er spændende, hvad eleverne har valgt som strategi til denne opgave. Og spændende, om nogle mon forfalder til at betragte rumfang af flyttekasse op mod rumfang af trailer. Et sjovt eksempel på, hvor virkelighedens verden og matematikkens verden møder hinanden. Vi tænker ikke, at opgave 3 er en oplagt opgave til GeoGebra. Og vi ser opgaven som en god anledning til at få en snak med eleverne om, hvornår en håndtegnet skitse måske er det hurtigste. Det betyder ikke, at elever, som er meget fortrolige med at tegne i programmer som GeoGebra ikke sagtens kan gøre det.

Statistikværktøjer i GeoGebra

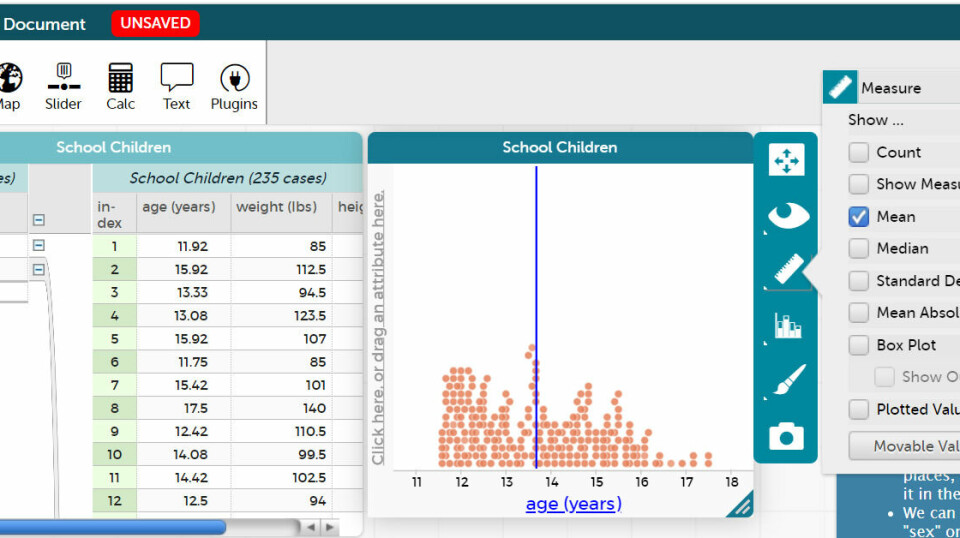
Opgave 4 handler om at analysere datasæt af forskellig størrelse. Eleverne får data i et regneark, og vi hæfter os ved, at der er ret mange data, særligt i det ene datasæt. (70 data). Disse data kunne eleverne fx sætte ind i GeoGebras regneark, tegne boksplot (flervariableanalyse) og benytte værktøjets muligheder for at få beregnet deskriptorer (Vis statistik).

Eleverne kan også databehandle i et regneark - det handler om, hvilke værktøjer eleverne er mest fortrolige med. Det er en interessant opgave, hvor eleverne selv skal gøre noget med de to datasæt for at vise noget matematik. Der ligger mange gode snakke til den daglige undervisning om netop datasæt af forskellig størrelse, om outliers, om argumenter og begrundelser for forskellige synspunkter, som jo netop er det smukke ved statistik.

Grafer for ikke-lineære sammenhænge i GeoGebra

I opgave 5 er der en funktionsforskrift og en tabel for en ikke-lineær sammenhæng, nemlig en andengradsfunktion. Vi hæfter os særligt ved opgave 5.3, hvor eleverne skal undersøge, hvilken fart bilen skal køre med for at udlede mindst CO2 pr. kørt kilometer. Her er det oplagt at tegne grafen og se, hvor f(x) er mindst. Måske kender nogle elever til toppunkt eller ekstremum, som findes under punktværktøjerne. Grafen giver et godt udgangspunkt for at undersøge her, hvor eleverne får et overblik over de data, som tabellen fx ikke viser.

Kender eleverne ikke ekstremumværktøjet, kan de jo slet og ret lægge et punkt på den tegnede graf, flytte rundt på det og se hvor y-værdien er mindst.

Symmetriaksier og firkanter

I opgave 7 skal eleverne undersøge, om de kan tegne firkanter med 0, netop 1, netop 2 og flere end 2 symmetriakser. Denne opgave forestiller vi os vil have været oplagt at løse i GeoGebra for mange elever. Eleverne kan tegne firkanter, tegne symmetriakser og undersøge med spejlingsværktøjet, om de tegnede firkanter nu også har en symmetriakse, hvor de har tegnet den.

I FP10 finder vi også en række spændende opgaver.

Kan man tegne præcist, måle og svare?

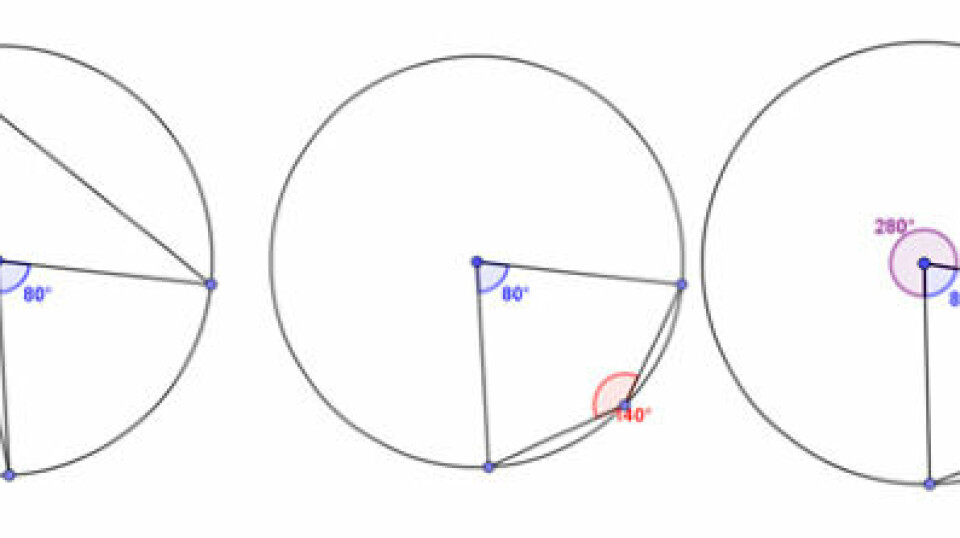
Opgave 2 er en opgave, som kalder på trigonometri. Vi tænker dog også, at de elever, som er fortrolige med at konstruere i GeoGebra kan komme langt i denne opgave ved at tegne præcist og argumentere ud fra tegningerne. Det kalder dog på netop præcisionen her - og at eleverne har gode vaner for konstruktion - bl.a med at bruge vinkelrette linjer og at afsætte vinkler korrekt. For små unøjagtigheder her kan betyde meget. Vi forestiller os, at mange elever også kunne vælge at bruge en trekantsløser. Med god præcision vil eleverne kunne tegne sig frem til flere af svarene i opgave 2. Men for de elever som har en god forståelse af trigonometri og egenskaber i retvinklede trekanter, kan de også løse opgaverne alene ad den vej.

Kan 3D i GeoGebra være en vej som alternativ til algebra?

Opgave 3 er en 1-spørgsmålsopgave, hvor eleverne skal give forslag til hvilke mål tre regnvandsbeholdere kan have, som opfylder et rumfang på 1 m^3 og en højde på mellem 0,5 og 2 m. Der skal være en kasseformet beholder, en cylinderformet beholder og en keglestubeformet beholder.

Er dette en oplagt GeoGebra-opgave? Nej ikke som sådan. Slet ikke til keglestubben. Men vi hæfter os ved, at der er 9 point i opgaven, så de elever, som ikke kan overskue formler, vil helt sikkert kunne komme et stykke af vejen i GeoGebra. De kan tegne en kasse i 3D - måle rumfang og justere på højde, længde og bredde indtil rumfanget passer. Det samme gør sig gældende for cylinderen. Skulle man ud i keglestubben, skal man tegne to kegler oven i hinanden og trække de to rumfang fra hinanden. Det er nok ikke den smarteste vej at gå, men det er dog muligt, hvis man afskrækkes af en formel med 3 ubekendte, pi og potenser.

De bedste værktøjer i 3D vil være udtræk til prisme/cylinder. Så den gode strategi vil være at konstruere sin grundflade i 2D-vinduet. Hoppe i 3D og udtrække til prisme, cylinder og evt. kegle.

Statiske eller dynamiske konstruktioner i undervisningen?

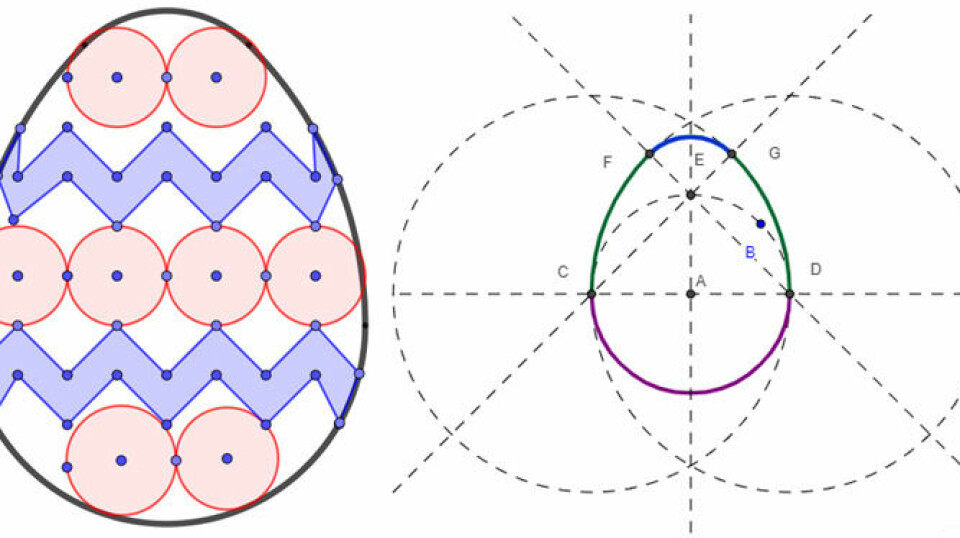
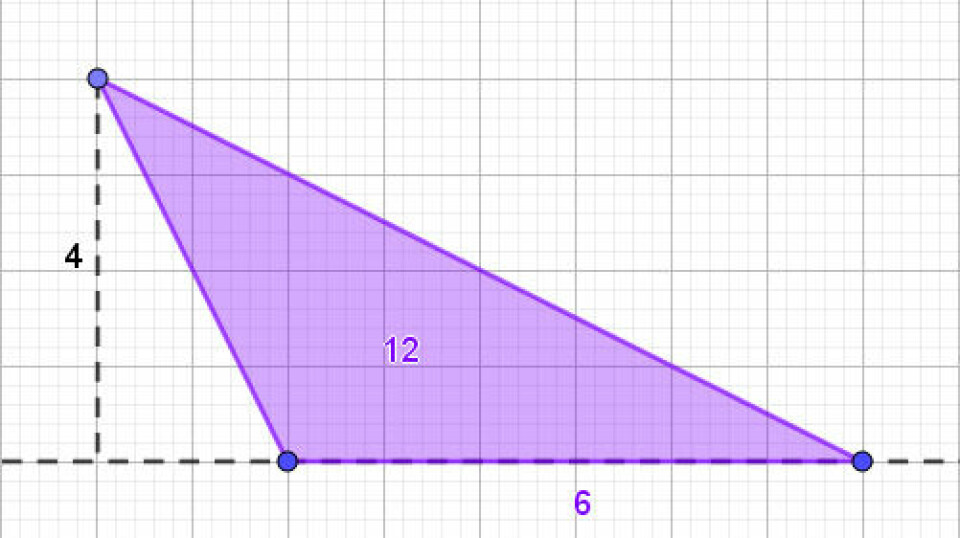
Opgave 6 er en opgave, som helt tydeligt kalder på et geometriprogram. Eleverne skal på et tidspunkt tegne en retvinklet trekant og tegne trekanter uden om den retvinklede trekant ud fra en opskrift, som vises i opgaven. Eleverne skal vise noget om sammenhængen mellem arealet af den retvinklede trekant og arealet af den trekant der dannes ud fra opskriften. De skal endvidere undersøge, om denne sammenhæng altid gælder. Hvis eleverne har lært gode konstruktionsvaner og får konstrueret den første trekant så den er dynamisk og retvinklet, og hvis de i de øvrige konstruktioner fortsat bruger gode konstruktionsvaner, kan de rimelig enkelt gå fra den første trekant med bestemte mål til mange andre eksempler i undersøgelsen.

Det ville kalde på at bruge linjestykke og ikke linjestykke med given længde. At lægge punkter på en linje og at bruge cirkler for at gøre linjestykker dobbelt så store. Vi har lavet en lille konstruktion her, I er velkomne til at kigge ind i. Det at arbejde med dynamiske konstruktioner er ikke noget, eleverne af sig selv finder på i en prøvesituation. Det kalder på, at man har arbejdet med dynamiske konstruktioner mange gange i undervisningen - i hele skoleforløbet, og det er givet godt ud, fordi en del af det generaliserende arbejde, jo kan understøttes så fint af dynamisk geometri, hvor vi udnytter de dynamiske egenskaber.

Kan man bevise i GeoGebra?

Opgave 7 handler om algebra og geometri. Regneudtryk, kvadrater og rektangler. Eleverne skal forholde sig til regneudtryk som de senere møder repræsenteret i kvadrater og rektangler, altså møder en kobling mellem geometri og algebra. Endelig skal de bevise at en omskrivning af det algebraiske udtryk altid er noget bestemt. Der er i hvert fald to veje at gå, som vi ser opgaven.

1. De kan fx gå i CAS og få CAS til at omskrive udtrykket og på den måde bevise. Eleverne kan også omskrive på egen hånd. Men GeoGebras CAS-vindue kan omskrive algebraiske udtryk.
2. De kan gå geometrisk til værks og betragte kvadratet og rektanglet og ud fra det lave et geometrisk bevis/ræsonnement, som også kan føre opgaven i mål. Faren er dog, hvis eleverne kommer til at fokusere på bestemte værdier og ikke betragter figurernes arealer med variable.

Men det er ikke en god vej at gå, at arbejde med tal i stedet for variable. Gad vide, om nogle elever mon har forsøgt at bevise ved at sætte taleksempler ind i udtrykket?

Hvad peger ind i næste års årsplan?

Det er to spændende opgavesæt eleverne har mødt i år, og der er rig mulighed for at arbejde med digitale værktøjer i prøvesituationen. Det spændende er, at prøverne i høj grad, som vi ser dem, afspejler det, der beskrives i læseplanen. Men i prøverne er der konkrete eksempler på opgaver og måder at arbejde på, som måske er mere overordnet beskrevet i læseplanen. Der er også opgaver, som peger ind i regneark og CAS, men vi har udelukkende her fokuseret på opgaver, hvor dynamisk geometri kan spille en rolle.

Hvilke tanker om kommende skoleårs matematikundervisning gør du og dine kolleger dig ud fra det, I har set i prøverne? Og har I mon haft gode drøftelser med jeres elever efter prøverne om, hvilke strategier og løsningsmetoder, de valgte under prøven?