Konstruktion eller tegning?

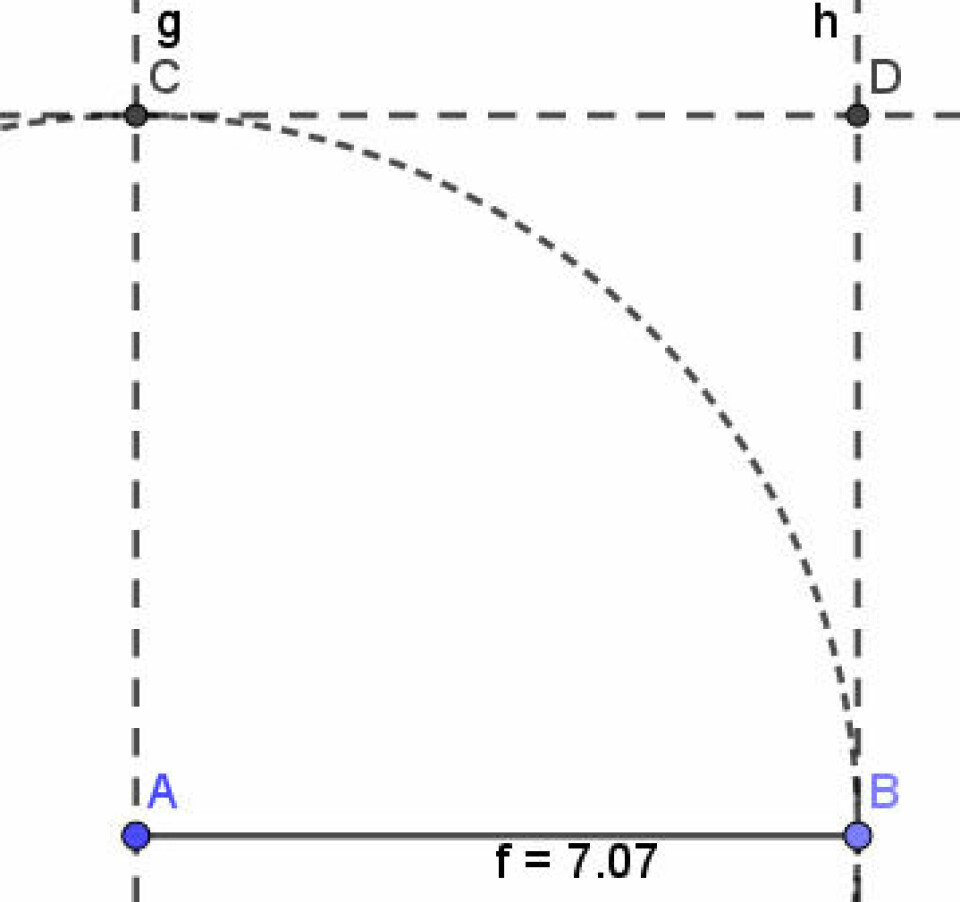
Forleden dag oplevede jeg en pige i 7. klasse være frustreret over en konstruktionsopgave. Hun skulle konstruere et kvadrat med areal 50 og ville bruge GeoGebra. Hun havde overblik over, at sidelængden i kvadratet skulle være kvadratroden af 50, og at det ikke var et pænt tal. Vi fik en snak om at den slags ikke-pæne tal hedder irrationelle tal.

Men hun var frustreret over GeoGebra. For kvadratroden af 50 passede ikke pænt i gitteret. Da jeg kiggede hende over skulderen for at se hendes konstruktionsteknik, blev det klart, at hun langt hen ad vejen brugte gitteret til støtte. Og jeg har ofte tænkt på, om det baggrundsgitter bliver et begrænsende sikkerhedsnet for vores elever nogle gange. Man kommer til at 'tegne' i gitteret i stedet for at tænke over, hvilke egenskaber, den figur, man skal tegne eller konstruere egentlig har. 

Med gitteret slukket var hun fri til at tænke i at hun skulle bruge et linjestykke med en given længde, nemlig kvadratroden af 50, som kan skrives sqrt(50). Derefter kunne hun bruge regulær polygon og til sin store glæde se, at arealet blev 50, som hun jo havde forventet. Vi fik også en snak om, at man kunne have konstrueret hele kvadratet med vinkelrette linjer, afsat en længde på linjerne, ved hjælp af et cirkelværktøj, fundet skæringspunkter mm. Tænk at et kvadrat med areal 50 kan rumme så mange fagord og begreber. 

Jeg oplever, at både elever og lærere er tøvende med at konstruere med de konstruktionsværktøjer, der er, fx vinkelrette linjer og parallelle linjer. At en afstand, som ikke er vandret faktisk bedst konstrueres som en cirkel ud fra punkt og radius. Måske kan vi få fat i nogle af definitionerne ved de forskellige geometriske figurer ved at dyrke netop den klassiske konstruktion af dem.

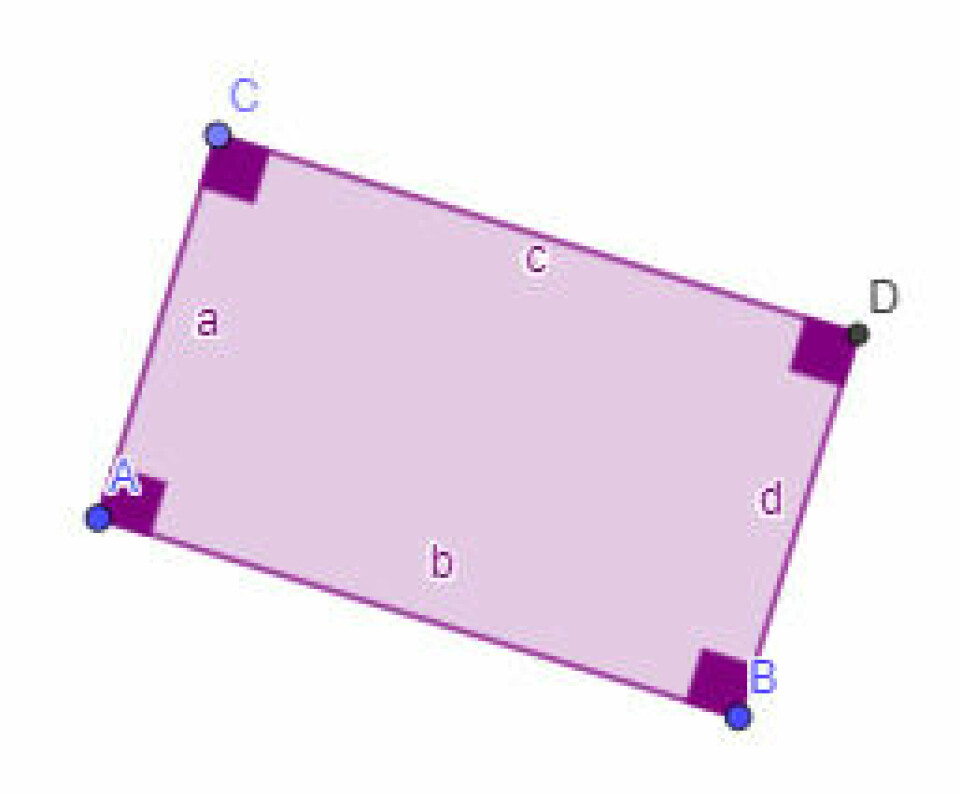
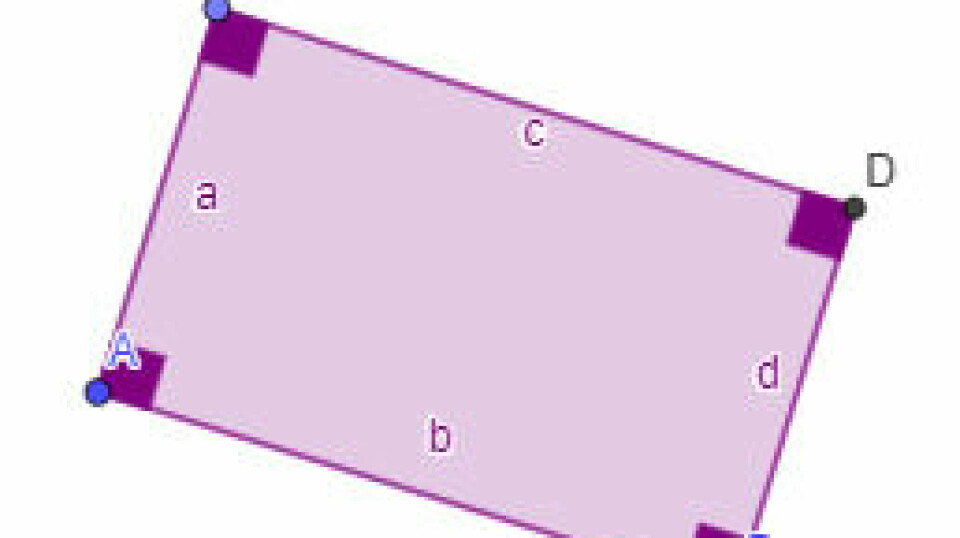
Forestil jer, at I skal konstruere et rektangel, som ikke kan trækkes ud af form. Dvs. det ophører aldrig med at være et rektangel, men du kan godt ændre længde og bredde i rektanglet. Det kan ligge på skrå i tegneblokken, men på intet tidspunkt ophører det med at være et rektangel. Hvordan skal sådan en konstruktion sættes sammen? Hvilken definition er der egentlig på et rektangel? Tip: hjælpeværktøjer kan være vinkelret linje, parallel linje mm. Prøv selv. Ellers er der en fil her, du kan hente ned og kigge lidt på konstruktionen bag.

Den slags øvelser kan give et godt blik for figurernes egenskaber, og der er gode muligheder for frugtbare matematiksnakke undervejs.

Her er et par forslag til gode figurer, man kan konstruere i tegneblok uden gitter. Alle figurer skal tænkes som dynamiske figurer - altså figurer, hvor man kan justere længde, bredde mm.

• Et kvadrat, som altid er et kvadrat, uden at bruge regulær polygon.
• Et rektangel som altid er et rektangel.
• Et parallelogram, som altid er et parallelogram.
• En retvinklet trekant, som altid er retvinklet.
• En ligebenet trekant, som altid er ligebenet.
• Et trapez, som altid er et trapez.
• En rombe, som altid er en rombe.
• En ligesidet trekant, som altid er ligesidet, uden at bruge regulær polygon.

Find gerne selv på flere.

God arbejdslyst.