Matematikkonsulenternes blog
Blog
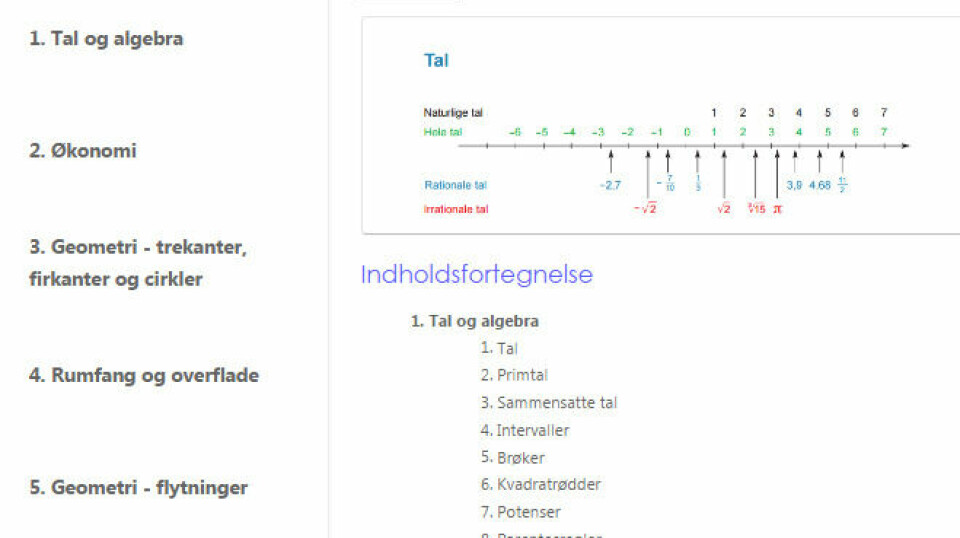
Ræsonnementer i undersøgende arbejde med GeoGebra
Hvordan kan vi arbejde med ræsonnementer i undersøgende arbejde med brug af GeoGebra?
En matematiklærer eller et menneske, som er glad for matematik holder ofte af at lede efter mønstre eller systemer i tingene. Mønsterdetektiver refererer Kjersti Wæge til i bogen Motivasjon i Matematikk fra 2018.
Det kan kalde på en særlig glæde, når vi kan omsætte til formler og beskrive særlige systemer. Sådan en æstetisk oplevelse, hvor verden lige blev lidt smukkere for en stund. Formler er jo smukke. Når de giver mening.
Men skal ræsonnementer altid omfatte generaliseringer og formler? Kan vi nogle gange arbejde med ræsonnementer, hvor det ikke indebærer algebra? Jeg tænker også, at den slags ræsonnementsarbejde har sin berettigelse.
Jeg vil prøve at se på et eksempel, som jeg mener, man kan arbejde med både på mellemtrinnet og i udskolingen, og så vil jeg forsøge at diskutere, hvilke former for ræsonnementer, der kunne komme ud af arbejdet.
Lad os betragte geometriske figurer, hvor areal og omkreds er lige store.
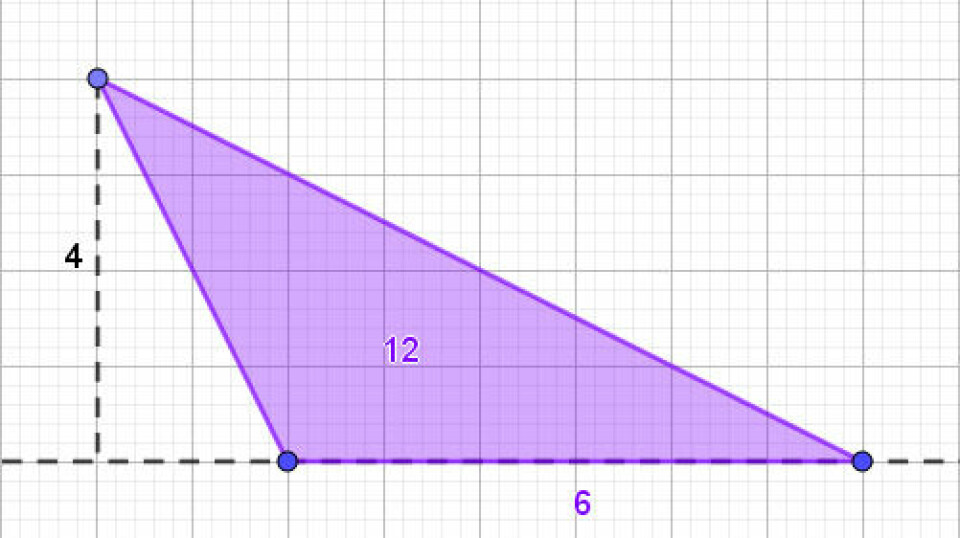
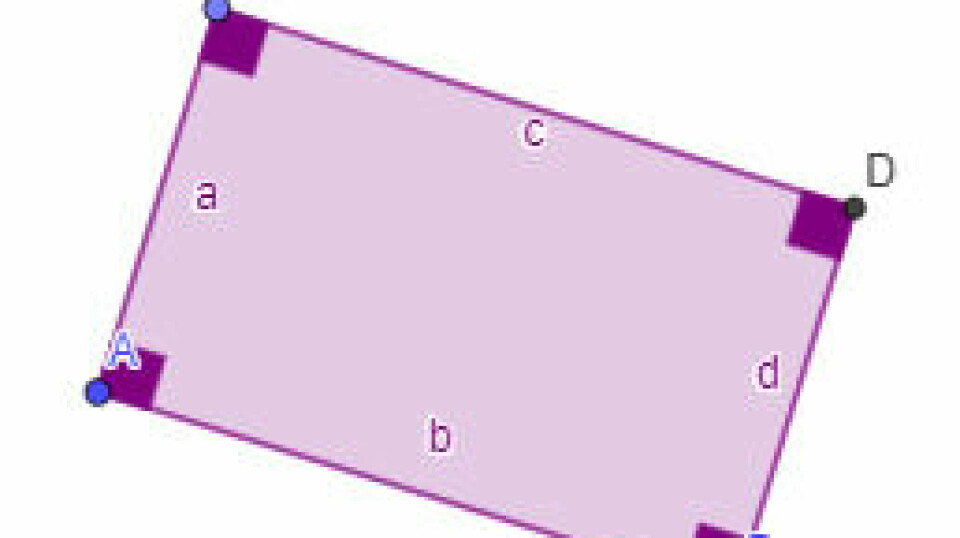
Vi kan fx starte med at betragte rektangler. Kan vi konstruere eller forestille os et rektangel, hvor areal og omkreds har samme værdi? For at undersøge det må vi jo nødvendigvis starte et sted. Hvis vi nu undersøger et rektangel, hvor den ene side er 8, er det så muligt?
Eleverne kan tegne i GeoGebra, måske må vi have en snak om, hvad et rektangel egentlig er, men det forudsætter, jeg, at vi godt ved her. De vil nok finde frem til, at hvis den ene side er 8, vil et rektangel med sidelængder 8 og 3 give et areal på 6*3 = 18 og en omkreds på 3 + 6 + 3 + 6 = 18. Det kan altså lade sig gøre.
Det var et tilfælde. Gælder det mon i flere tilfælde?
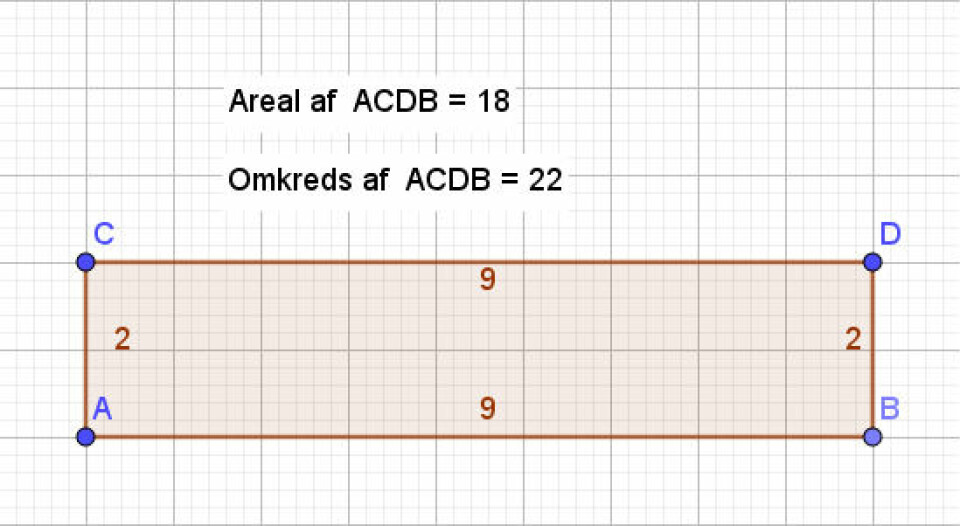
Hvis nu en sidelængde i stedet var 9? Her vil eleverne måske starte med heltallige løsninger. Hvis de lader den anden side være 2, får de:
Her er omkredsen større end arealet.
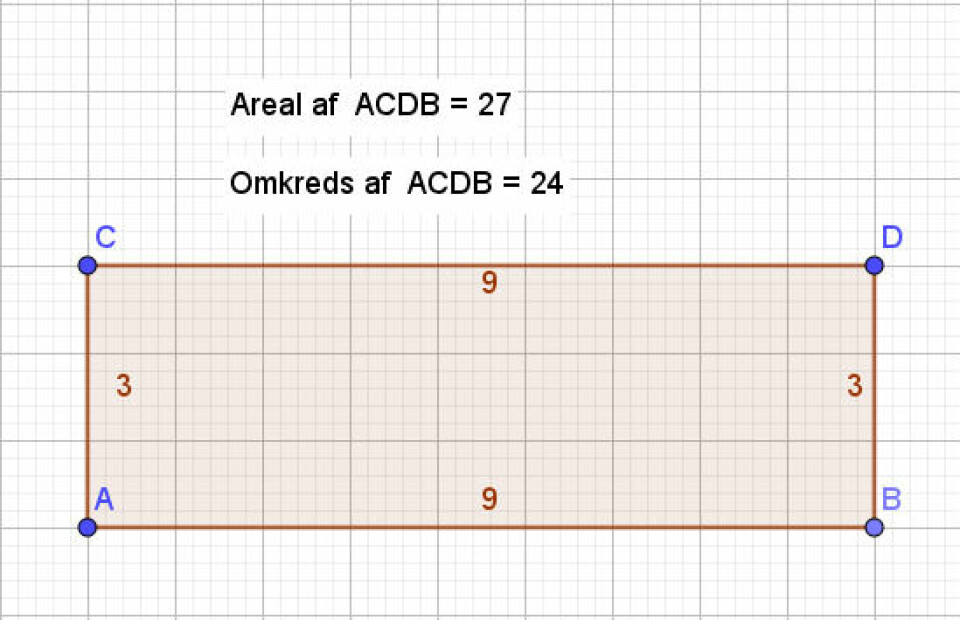
Forsøger de med sidelængde 3, får de:
Og her vil eleverne se, at de to har byttet plads, nu er arealet større end omkredsen.
Kunne vi tale med eleverne om, hvad de tænker om det? Kunne det tænkes, at der var et tidspunkt, hvor de to størrelser altså var lige store, hvis det nu er modsat vores tilfælde fra før?Eleverne kan trække lidt frem og tilbage - måske zoome ind, men det er min oplevelse, at de fleste kan overbevise sig selv om, at det må kunne lade sig gøre. Nogle elever med tilpas god tålmodighed vil også kunne finde løsninger.
Eleverne vil, hvis vi udfordrer dem til det, kunne sætte ord på det de ser, nemlig at i starten er omkredsen større end arealet, men efterhånden overtager arealet - og hvis de fortsætter længe nok, ser det ikke ud til, at omkredsen overhaler arealet igen. Derfor må de jo nødvendigvis være lige store på et tidspunkt. Jeg er med på, og det er læseren sikkert også, at man rimelig enkelt kan oversætte dette til ligninger og algebra. Men behøver vi altid det?
Er dette, jeg har beskrevet et ræsonnement? Jeg mener, at det er et ræsonnement, og det er min oplevelse, at GeoGebra kan støtte den her slags ræsonnementer. Men det kræver, at vi sætter eleverne i situationer, hvor de skal undersøge noget ved at se på tallene/enkelteksempler og på den baggrund forsøge at beskrive det, de observerer. Det kræver igen, at eleverne øver sig i at observere og lægge mærke til ting. Det centrale for mig er, at eleverne sættes i situationer, hvor de skal argumentere ud fra det, de ser og erfarer på skærmen. Og de skal lytte til og forholde sig til hinanden argumenter.
Analyse af matematikholdige situationer kan omfatte andet og mere end algebra og ligninger, og med dynamisk geometri skal vi huske at udnytte netop evnen til hele tiden at observere, hvordan værdierne ændrer sig, når vi justerer noget, sådan at den form for argumentation også får mulighed for at have værdi en gang i mellem i matematikundervisningen. Ikke alle situationer lader sig til alle tidspunkter løse med flotte ligninger eller formler, og jeg ville holde sådan af, at vi fik skabt plads til at argumentere ud fra systematiske observationer i dynamisk geometri ind i mellem.
Et par små forsøg læseren selv kan gøre sig er, fx at overveje, om det er muligt at tegne en cirkel, hvor areal og omkreds er lige store uden at gå algebraisk til værks. Eller lidt mere krævende, kan man tegne en trekant, hvor omkreds og areal er lige store? Hvordan vil du starte sådan en undersøgelse? Hvordan vil en elev i 5.-7. klasse gøre det?
Hvis du har lyst, kan du jo kigge med i denne fil, hvor der godt nok er dykket ned i en særlig type trekant, for at få et sted at starte. https://www.geogebra.org/m/tqetc4yg
Trekanterne giver i hvert fald nogle situationer, hvor det ikke lige så nemt som med rektangler lader sig opstille i ligninger, som vi kan løse, hvis vi var elever i 5.-7. klasse.
Hvordan arbejder du selv med ræsonnementer i dynamisk geometri? Del gerne dine erfaringer herunder.