Teknik eller forståelse?

Digitale værktøjer som bl.a. dynamisk geometri omtales i læseplanen, men også regneark, cas, lommeregner og andre værktøjer indgår i de formelle tekster.

Der nævnes ikke specifikke programmer som GeoGebra, Excel, Sheets, Wordmat, MatematiKAN, Calcme eller lign. i de formelle tekster fra ministeriet, så det er op til skolerne at finde ud af, hvilke værktøjer, de ønsker at anvende.

I flere lærerfora, hvor lærere hjælper hinanden didaktisk, teknisk og på andre måder, dukker jævnligt spørgsmål op, som peger i retningen af, at lærere efterspørger, om der er et smart fix i værktøjet, så det lige kan løse et bestemt matematisk problem. Hvad skal jeg skrive i værktøjet for…? Eller hvordan jeg kan jeg få … til at løse …? Det kan være svært at tage diskussionen om værktøjets rolle, når deltagere i et forum beder om hjælp, og man bør måske endda undlade at gå ind i den. Derfor vil vi i stedet tage temaet op her endnu engang, så vi forhåbentlig kan sætte nogle tanker i gang om, hvordan vi på bedst mulig vis udnytter de digitale værktøjers potentialer.

Diskussionen om opgaverne fra afgangsprøverne.

Lige nu diskuterer mange matematiklærere nogle af opgaverne fra decemberprøverne i 2020. Det efterspørges om nogle af værktøjerne kan løse en ligning med tre ubekendte. Nogle værktøjer kan, andre kan ikke, men ingen af syntakserne for at kunne løse den slags ligninger er lette at gå til for eleverne. Nogle lærere spørger til, om det forventes, at eleverne kan anvende fx CAS-værktøjer på den måde i folkeskolen, og man fornemmer måske et gisp over, om man måske har sovet i timen, eller om man måske ikke har lært eleverne det, der forventes. Men læseplanen foreskriver ikke så specifikke kommandoer eller funktioner, så det vil altid være op til lærerens eller fagteamets egen fortolkning, hvad eleverne skal kunne i de forskellige programmer. Det må dog aldrig blive et mål i sig selv at kunne indtaste en bestemt syntaks for at få maskinen til at spytte det korrekte resultat ud. Så har vi fokus det forkerte sted, nemlig på maskinbetjening frem for på udvikling af forståelse af de matematisk koncepter.

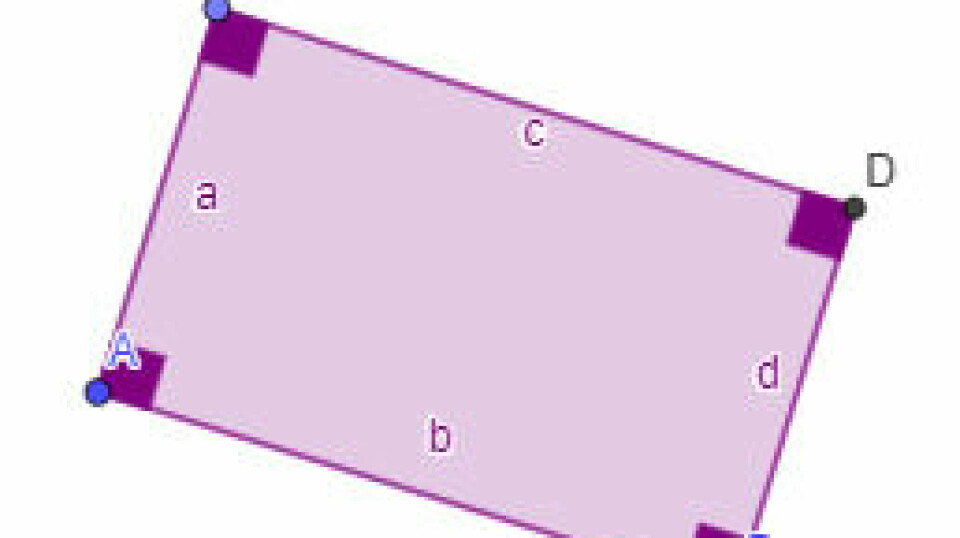
Der har også været drøftelser af opgaven med bestemte geometriske figurer med arealet 50. Kan man få GeoGebra til at lave en figur med et ønsket areal, blot ved at indtaste arealet? Altså bare få tegnet et rektangel med areal 50 eller en ligesidet trekant med areal 50? I det spørgsmål ligger samtidig en forventning til det digitale værktøj som noget, man udliciterer matematikken til, så man ikke selv behøver at være stiv i de geometriske egenskaber og sammenhænge, som er det, opgaven peger ind i. Værktøjet bruges til at få eleverne til at tænke mindre. Det var ikke lige det, der var meningen med de digitale værktøjer i matematikundervisningen.

For mange deltagere i disse fora, handler spørgsmålene dog også om en tørst efter selv at blive klogere på programmernes funktionaliteter. Det er forfriskende at se, at mange gerne vil forfine egne teknikker og blive endnu klogere på de forskellige digitale værktøjer, der benyttes i undervisningen. Og det er lige så forfriskende at se, hvordan mange hjælper hinanden og bidrager med videovejledning og gratis resurser til hinanden online.

Det er prøvetid lige om lidt. Vi venter alle i spænding på at se, hvad årets prøvesæt i fagene kaster eleverne ud i, og måske er spændingen lidt ekstra intens i år, fordi eleverne i 9. og 10. klasse har været fjernundervist en relativt stor del af tiden.

Det er altid velkomment og vigtigt at drøfte, hvad vi skal med de digitale værktøjer, men vi tror på, at det er yderst vigtigt, at vi husker os selv og hinanden på, at vi aldrig må fortabe os i at lære eleverne svære og specifikke syntakser, som passer på få og snævre problemstillinger, men i stedet underviser med henblik på, at eleverne udvikler forståelse for fx geometriske egenskaber og sammenhænge, tal og algebra, statistik og sandsynlighed mm. Forståelse må gå forud for alt andet. Der gemmer sig nærmest uendelige muligheder i komplekse syntakser og finurlige måder at opstille ligninger, sekvenser eller andet godt på i de digitale værktøjer, men det kan blive så komplekst, at eleverne står af undervejs. Og kan de overhovedet genkalde sig den syntaks i prøvesituationen, hvis det er noget de måske har set en enkelt gang før?

Derudover er det også vigtigt at huske på, at de, der udvikler prøverne, også godt kender til de digitale værktøjer og ofte spørger på andre måder, netop for at teste forståelsen og ikke bare, om eleven kender en bestemt syntaks i et digitalt værktøj.

Kun de, der fremstiller prøverne, kender indholdet, der kommer, og vi kan derfor ikke forberede vores elever til at være klar med særlige syntakser, der vil passe til lige netop de problemstillinger, der dukker op. Men vi kan forberede dem på at løse problemer.

Hvis vi kigger på problembehandling, så handler det om at kunne løse matematiske spørgsmål, der ikke kan besvares udelukkende med rutinemetoder. Ofte kræver løsning af matematiske problemer en eller anden form for undersøgelse.

Øvebaner til matematiske problemer.

Kan man så øve sig så meget i at løse matematiske problemer, at det i sig selv bliver en form for rutinemetode? Det mener vi godt, at man kan. Eleverne kan stå i problemløsningssituationer mange gange, hvor vi samtidigt med problemløsningen også arbejder med elevernes metakognitive strategier og går i dialog med dem om deres strategi.

• Hvad kan du gøre for at komme i gang?
• Minder det om noget, du har prøvet før?
• Hvad ved du om emnet?
• Kan du prøve dig frem?
• Har du tænkt det hele med?
• Er der et særligt system?
• Er du systematisk i din undersøgelse?
• Kan dit resultat passe?
• Hvordan kan du kommunikere resultatet, så det bliver nemt at forstå, hvad du har tænkt og gjort?
• Osv.

Det er meget muligt, at eleverne kan trække på digitale værktøjer undervejs i problemløsningsprocessen, men det kan også være, at det for nogle elever er nemmere at gøre noget andet.

Dialogen om strategier er vigtig, for den dialog skal eleven føre med sig selv i prøvesituationen. Hvad skal jeg gøre her? Hvad har jeg gjort tidligere? Osv. Eleven kan overføre klassedialogen til en indre dialog i prøvesituationen og forsøge at finde en vej i problemløsningen på de måde. Selvom matematiske problemer er forskellige, kan der være mange lighedstræk i måden vi angriber dem på. 

Og skal man vægte den sparsomme tid, der er til prøverne, kunne netop det at give eleverne gode strategier til problemløsning være et sted at prioritere lidt af tiden. 

Vi har tidligere skrevet dette blogindlæg om at få eleverne til at tænke mere ikke mindre med GeoGebra, men vores holdning er den samme. Brug værktøjerne, så eleverne kan tænke mere over indholdet af matematikken. Og brug det på en måde, hvor der er fokus på forståelse af noget matematisk indhold. Fokuser på basale tekniske færdigheder i programmerne, da de burde være alt rigeligt. Det betyder dog ikke, at du ikke godt kan udfordre eleverne nogle gange ved at vise andre teknikker eller syntakser.

Lidt teknisk nørderi i GeoGebra.

Det er altid sjovt at udfordre sig selv i nye teknikker. Så her bringer vi en til dig - næsten dugfrisk fra det internationale GeoGebra Institut. Det er den nye PieChart Kommando i GeoGebra, der burde virke i alle opdaterede versioner af GeoGebra. PieChart({liste med frekvenser},(koordinater for centrum), radius).

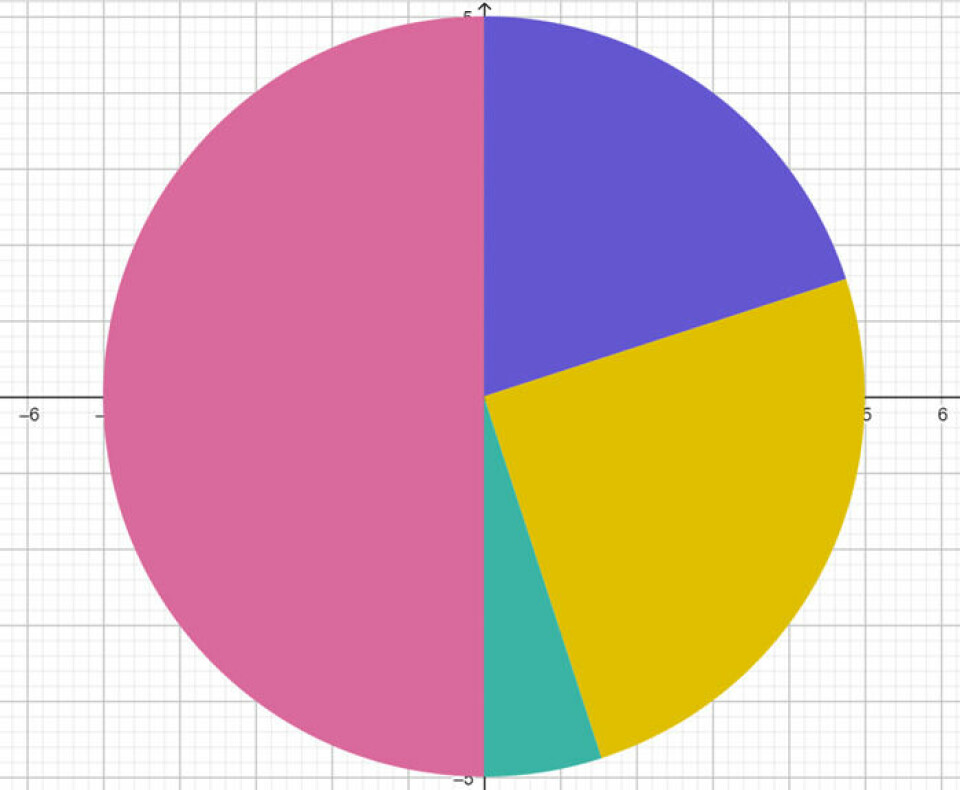
Fx PieChart({20,25,5,50},(0,0),5) - frekvenserne er altså 20 %, 25 %, 5 %, 50 %, centrum er i (0,0) og radius er 5. Men man skal lige huske Tuborgklammerne omkring listen af frekvenserne…

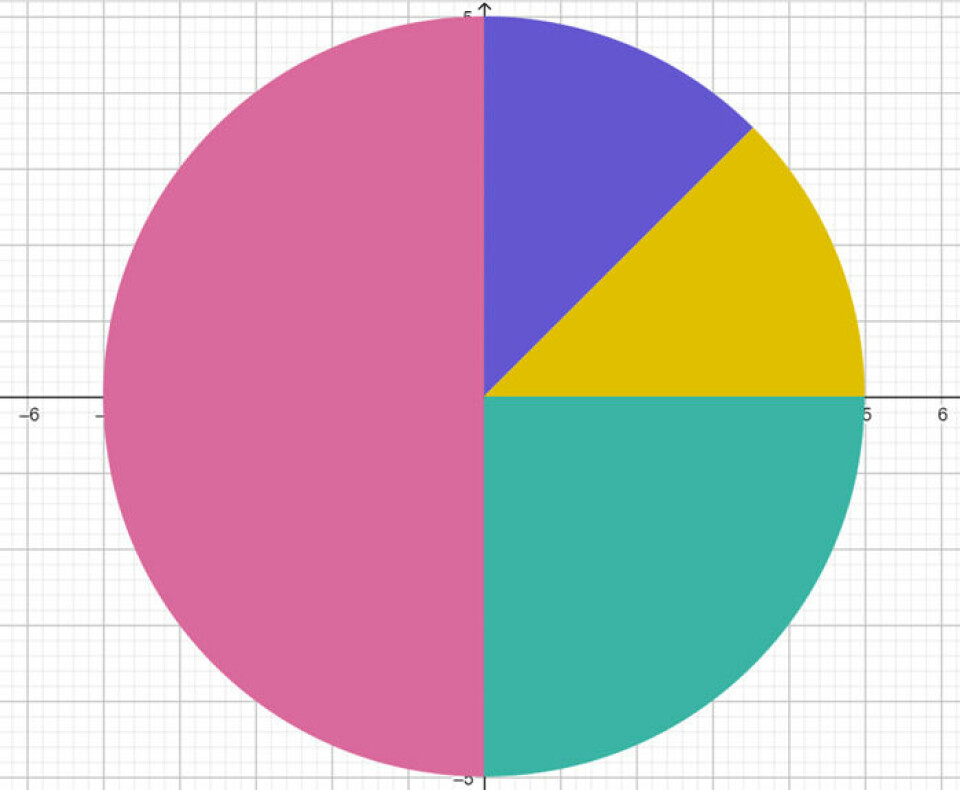
Meget kan gå galt endnu. Måske bliver det mere brugervenligt med tiden. Vi ville nok vælge at lade eleverne sammenligne arbejdet i det regneark klassen nu ellers bruger og så med GeoGebras måde. Man kan fx bede eleverne forholde sig til, hvilke farver der passer med hvilket tal i kommandoen. Herefter kan man ændre tallene til eksempelvis {1, 1, 2, 4}, der ikke tilsammen giver 100 og bede eleverne forklare, evt. på en skærmoptagelse, hvordan, de tror, GeoGebra har tegnet diagrammet. Gentag med sværere tal og bed til sidst eleverne om at generalisere, hvordan GeoGebra oversætter tallene i Tuborgklammerne til en række cirkeludsnit, der tilsammen danner en hel cirkel.

I eksemplet herover udnytter vi den enorme regnekraft i GeoGebra til at se mønstre og opdage sammenhænge i, hvordan programmet danner sådan et cirkeldiagram.

Har du selv gode fif eller erfaringer med at gøre dine elever trygge i problemløsning er du meget velkommen til at dele dem her - eller med en kær kollega.

Vi vil også rigtig gerne høre om dine erfaringer med teknik eller forståelse-dilemmaet her på bloggen.