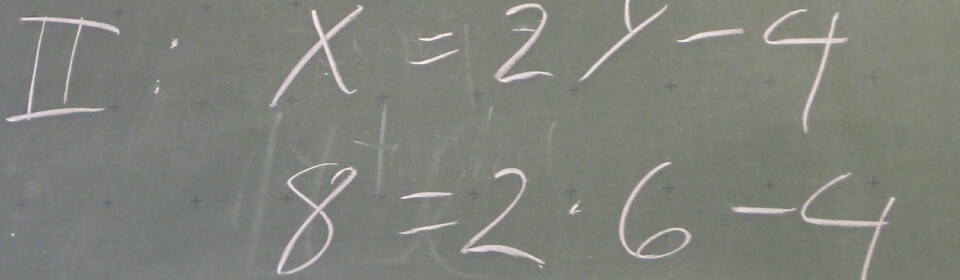
Matematikkonsulenternes blog
Blog

Hvad viser min graf?
Taler du med dine elever om kommunikationsværdien på grafer og diagrammer?
I årets prøvesæt i FP9 har eleverne skullet tegne en graf (FP9 opgave 5.2). Eleverne må selv vælge, hvordan de tegner deres graf, om de vil gøre det i hånden eller med et digitalt værktøj.
Opgaven i FP9-sættet lyder:
Tegn en graf, som viser sammenhængen mellem tiden og stearinlysets længde i al den tid, lyset brænder.
Eleverne har data i en tabel, som er udgangspunktet for den graf, de skal fremstille. Som beskikkede censorer har vi set en masse forskellige tolkninger af, hvordan sådan en graf kan se ud, og derfor vælger vi at skrive lidt om det her.
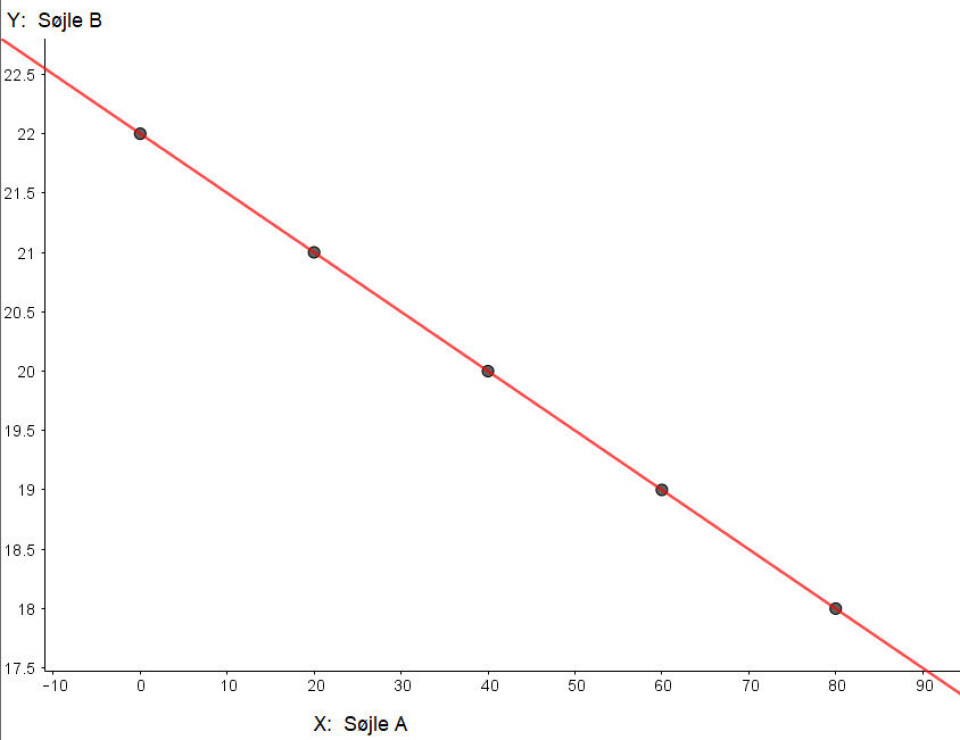
En stor del af eleverne vælger at bruge GeoGebra til opgaven. En del lægger tabellen i regnearket, laver regressionsanalyse og indsætter et screenshot fra regressionsanalysen. Så er der tegnet en graf. Men denne graf viser jo ikke nødvendigvis stearinlysets længde i al den tid, lyset brænder. Nogle har løst opgave 5.1 først, hvor de har skullet bestemme lysets længde efter 120 minutter, derfor er der flere punkter på deres regressionsplot, men heller ikke her viser de hele brændtiden (Se billedet Regressionsplot i GeoGebra til venstre).
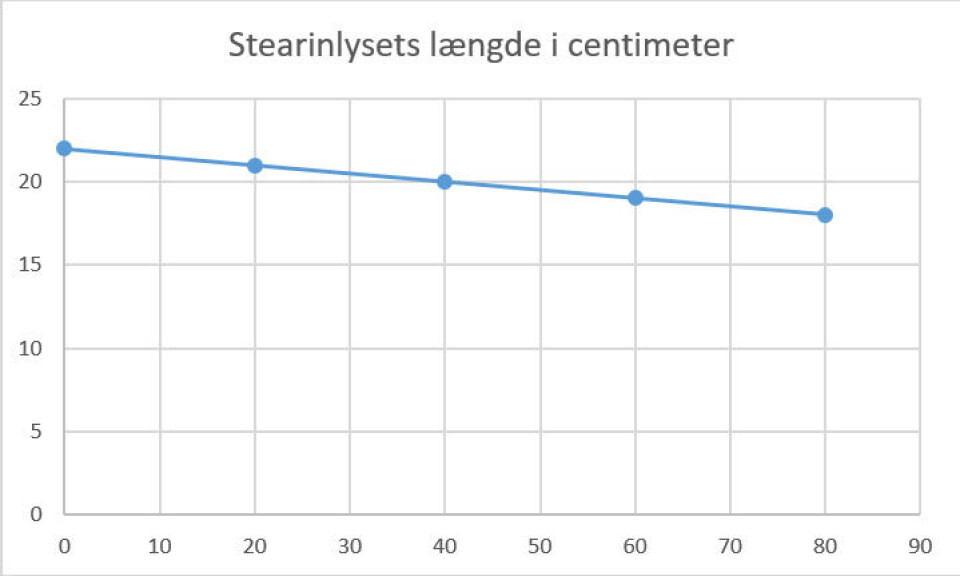
En tilsvarende model ser vi med elever, der går i gang i regneark. De tegner grafer i stil med denne (Se billedet Regnearksgraf).
Heller ikke her vises sammenhængen mellem tiden og stearinlysets længde i al den tid, lyset brænder, men udelukkende ud fra det datasæt der fremgår af opgaven.
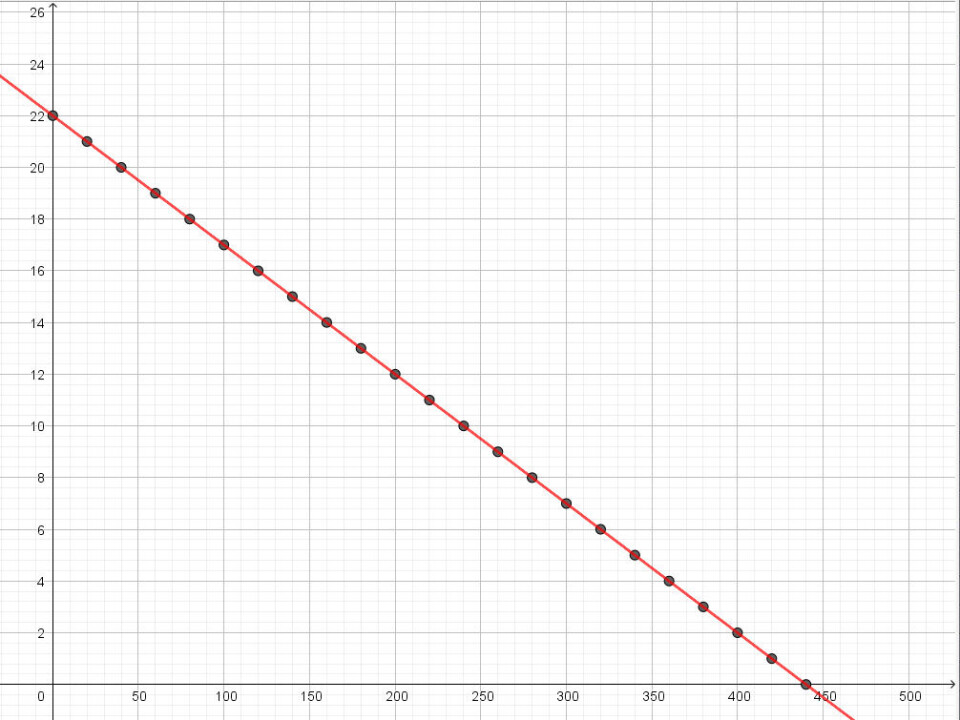
En del elever vælger også at tolke søjlediagram som graf og afleverer den her slags grafer (Se billedet Søjlediagram fra regneark).
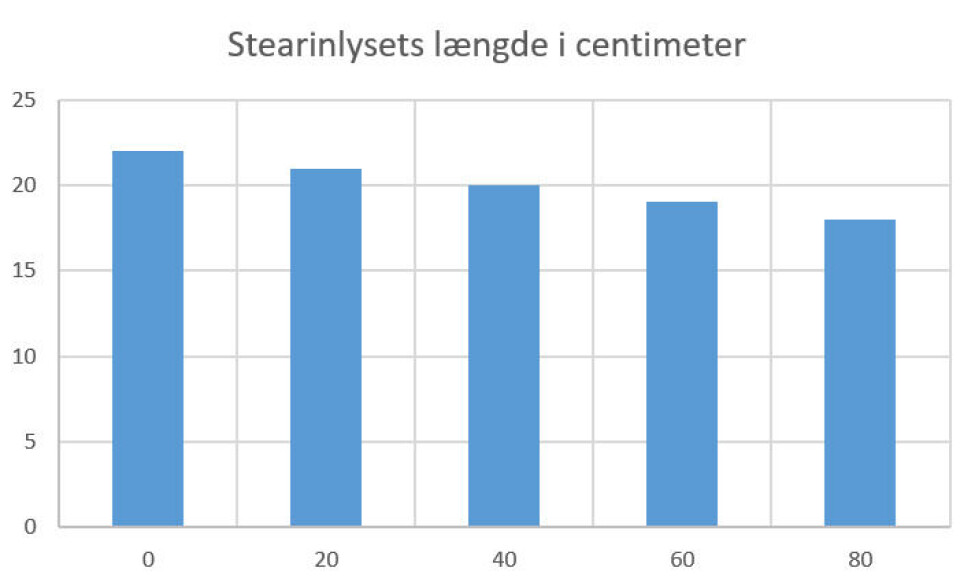
Man kan jo sige, at de viser øjebliksbilleder af lysets længde til forskellige tider, men søjlediagrammet er ikke en god graf her, da der ikke er tale om øjebliksbilleder. Lyset brænder jo konstant og vil derfor have faldende højde mellem de søjler, der er vist i diagrammet.
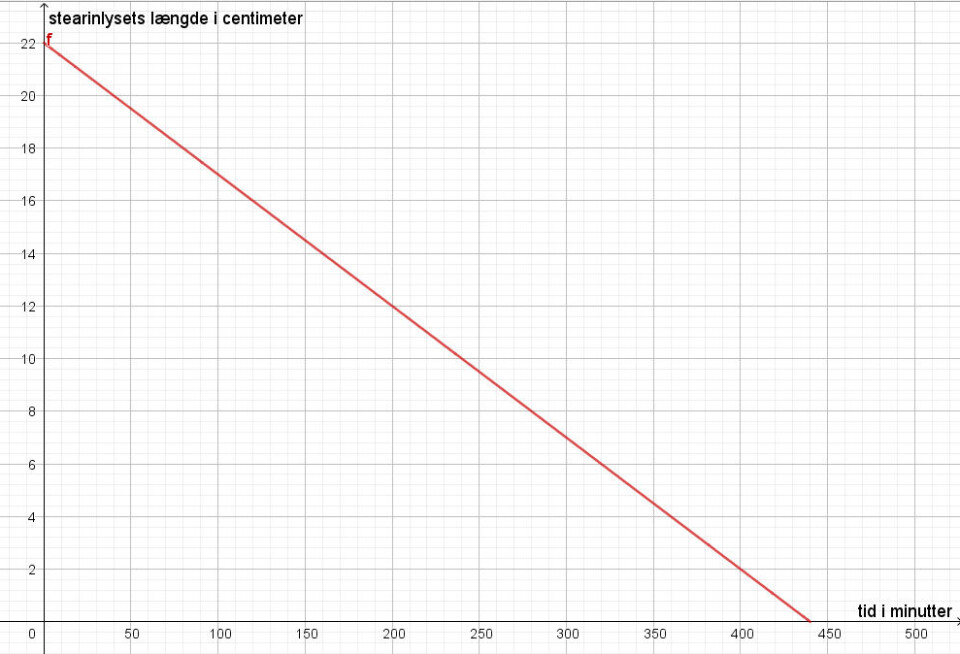
Der er også elever, som lykkes med at tegne en graf for hele lysets brændtid, og bliver vi i regressionsvinduet får de sådan en graf. (Se Regressionsplot fra GeoGebra herunder).
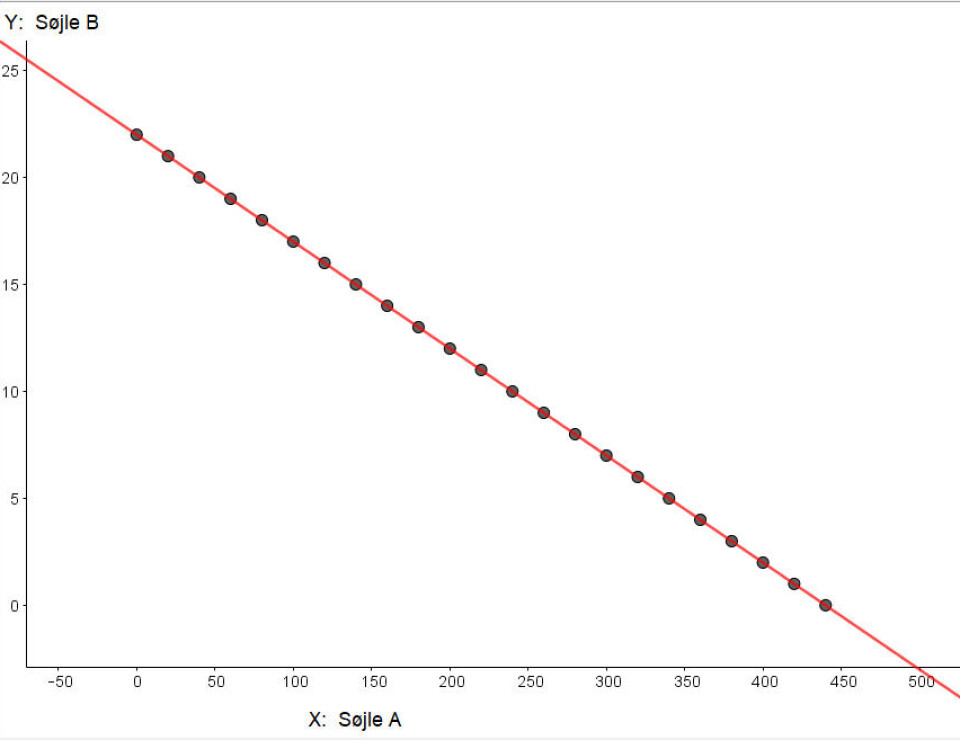
Vi bemærker, at regressionsvinduet generelt ikke er et godt værktøj til at tegne grafer. Det et godt værktøj til regression, men hvis det er en graf, der skal kommunikeres, vil det være en god idé at lægge grafen over i tegneblokken.
Vi ser også elever, som kommer så langt (se billedet: Regressionslinje overført til tegneblokken).
Der er nogle ting, som vi som beskikkede censorer vil opfordre til dialog om i de kommende matematiktimer.
I får det i punktform herunder
- Hvilke krav er der til min graf? Er der et bestemt interval, grafen SKAL dække?
- Hvilket interval er meningsfuldt for min graf? Kan der være negative værdier for x og y?
- Hvad viser mine akser? Hvad hører til på x-aksen og hvad hører til på y-aksen? Hvad er den uafhængige variabel og hvad er den afhængige variabel?
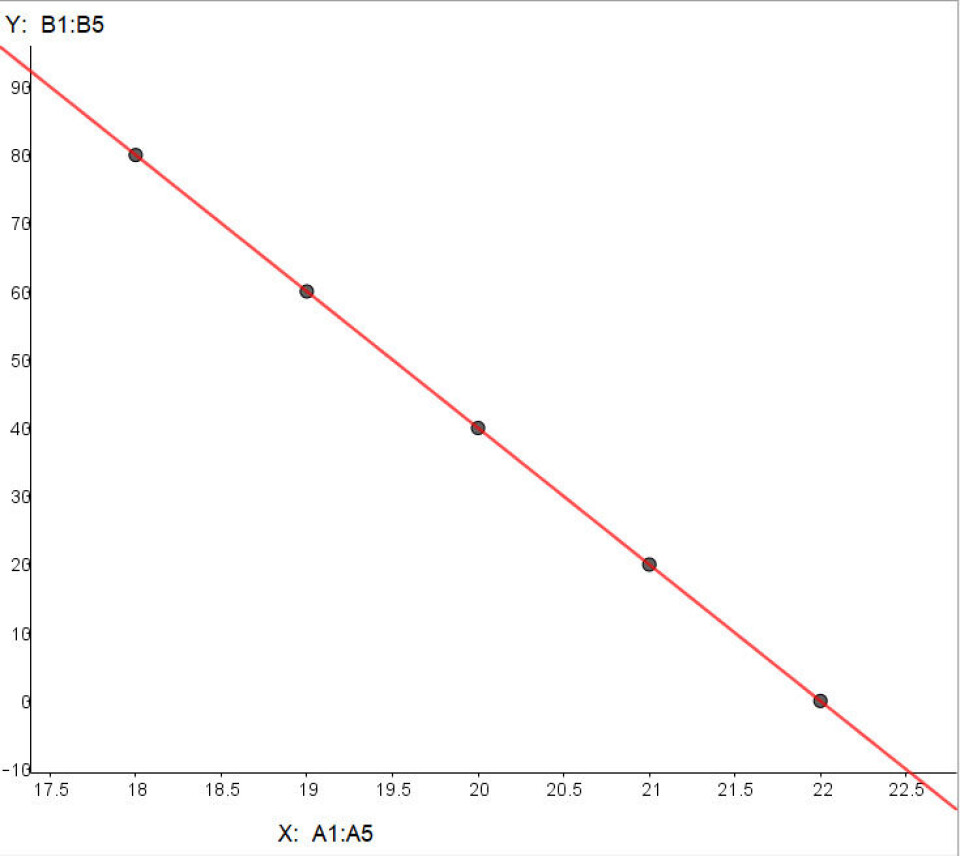
Der er en del elever, som bytter rundt på x og y og stadig får en ret linje, naturligvis, som ved første øjekast kan se fin ud, men som får vist at eleverne nok ikke har taget stilling til afhængig og uafhængig variabel. (Se billedet Omvendt regressionsplot).
Der er forståeligt måske vanskeligt for nogle elever.
Det, der har gjort mest ondt i censorhjertet har været at se, hvor få elever der rent faktisk tager stilling til, hvad akserne viser og sætter etiketter på akserne. Vores egen lommeundersøgelse fra de udsnit af landet, vi har rettet fra viser, at det er under 10 % af eleverne i år. Nogle få skriver på i hånden, hvilket er helt fint, andre sætter tekstbokse ind, andre igen bruger i regnearket de layoutværktøjer der er til grafer, hvis de arbejder i excel eller fx sheets. Det handler ikke så meget om en bestemt måde at gøre det på, men blot at få kommunikeret det til læseren.
Eleverne mister ikke point for opgaveløsningen hvis de ikke sætter etiketter på akserne, men det bidrager negativt til helhedsindtrykket. Så hvis eleverne ligger i et grænseområde kan det være en af faktorerne, som kan være med til at eleverne får en lavere karakter.
Vi har tidligere arbejdet med elever, hvor det drejede sig om, at de skulle få blik for at kommunikere grafer på en hensigtsmæssig måde. I den forbindelse kan vi anbefale en lille sorteringsøvelse, hvor eleverne udstyres med grafer som har forskellige mangler. I kan se et eksempel her.
Når eleverne skal lægge graferne i rækkefølge ud fra hvordan de er kommunikeret, får de som regel ret hurtigt øje på, hvad der fungerer bedre end andet. Hvis eleverne først selv har løst opgaven, derefter kigger på andres løsning og diskuterer i grupper, hvordan kommunikationen er bedst, og derefter skal gå tilbage til deres egen graf og foretage justeringer, så kommer det som regel på rygraden af, at der er nogle ting, man altid lige skal overveje, når man tegner/kommunikerer en graf.
De digitale værktøjer gør, at vi nemt kan producere grafer og diagrammer. Men når noget er nemt, må vi også bruge den ekstra kapacitet, vi opnår, til at være ekstra tydelige i vores kommunikation ved at kigge kritisk på grafen og tage stilling til, om den nu er vist på den bedst mulige måde.
Er det noget, du har fokus på med dine elever i den daglige undervisning? Del gerne dine erfaringer med os andre her i netværket.